С О Ц И Н Т Е Г Р У М

Недавно доктор Mitcheil Feigenbaum
http://www.rockefeller.edu/research/abstract.php?id=38

опубликовал статью, в которой он выводит преобразования Лоренца (лежащие в основе СТО) и релятивистский "закон сложения" скоростей, не используя при этом второй постулат Эйнштейна (одинаковость скорости света в движущихся с постоянной скоростью друг относительно друга системах отсчёта).

Фейгенбаум доказывает, что преобразования Лоренца логически НЕ связаны со вторым постулатом Эйнштейна и могли быть выведены уже Галилеем, если бы в то время имелся в распоряжении необходимый для этого математический аппарат.

ТЕКСТ СТАТЬИ:
Mitcheil Feigenbaum
"The Theory of Relativity - Galileo's Child" May 25; 2008.
http://arxiv.org/PS_cache/arxiv/pdf/080 ... 1234v1.pdf

NewScientist 29 October 2008 поместил статью
Mark Buchanon
Why Einstein was wrong about relativity (pp. 28-31)
где автор рассказывает об этом открытии.
http://www.newscientist.com/article/mg2 ... ivity.html

Он пишет:




Статья Фейгенбаума является как бы заключительным аккордом длинной истории публикаций, в которых шаг за шагом происходило постепенное отделение релятивистских эффектов от второго постулата Эйнштейна.
David Mermin ещё в 1985 году показал, что преобразования Лоренца можно получить не прибегая ко второму постулату:
N. D. Mermin (1984) Relativity without light, Am. J. Phys. 52; pp. 119-124.

В последние 5 лет на этй тему - выводу ТО без использования второго постулата Эйнштейна - было опубликовано несколько статей.
Например, в статье
C. R. Paiva и M. A. Ribeiro "Generalized relativistic velocity addition with spacetime algebra"
http://arxiv.org/ftp/physics/papers/0511/0511247.pdf

авторы пишут:

и дают алгебраический вывод преобразований Лоренца без использования второго постулата.

В статье
Palash B. Pal (2003) "Nothing but relativity"
http://arxiv.org/pdf/physics/0302045

дан вывод преобразований Лоренца без применения второго постулата - исходя лишь из свойств изотропности и однородности пространства и принципа относительности Галилея.

Мичел Фейгенбаум в заключении к своей статье приводит слова благодарности доктору Divid Mermin, который оказал большое влияние на разработку идей этой статьи дискуссиями и ценными замечаниями. Статью Мичела Фейгенбаума следует рассматривать как законченную формулировку течения, которое сформировалось в релятивистской физике в последние 40 лет - течение, которое пытается осмыслить релятивистские закономерности без использования второго постулата Эйнштейна. Вывести нетривиальные релятивистские эффекты исходя из принципа относительности Галилея и принципов симметрии (однородности и изотропии пространства). Самое удивительное состоит в том, что это оказывается не только возможно, но даже неизбежно.
Релятивистские эффекты - прямое следствие того, что во всех равномерно движущихся системах отсчёта действуют одни и те же физические законы механики, и пространство в каждой такой системе отсчёта однородно и изотропно.

Ход рассуждений в статье М. Фейгенбаума.

Фегенбаум доказывает, что принцип относительности Галилея и принцип изотропии пространства достаточны, чтобы вывести все релятивистские соотношения СТО.

При выводе естественным образом возникает некоторая константа с размерностью скорости, которая выполняет в полученных формулах ту же функцию, какую скорость света выполняет в формулах выведенных Эйнштейном. Но эта константа вовсе не обязательно должна быть равна скорости света. Второй постулат Эйнштейна (скорость света одинакова во всех равномерно движущихся системах отсчёта) не нужен для вывода релятивистских соотношений.

Приведём некоторые пункты, которые поясняют, как можно вывести преобразования Лоренца и релятивистское правило "сложения скоростей" без использования второго постулата Эйнштейна.

1) Сначала Фейгенбаум вводит соотношение:
r(v; V) – есть скорость тела относительно системы К’, которая движется относительно К со скоростью V. При этом v – скорость тела в системе К. V- скорость системы K' относительно К.

Фейгенбаум исследует, какие свойства имеет отношение r(v; V) исходя из принципа относительности Галилея и выводит ряд формул.

В частности, он доказывает следующие формулы:
(1) r(0;V) = - V – скорость К относительно К’ противоположна скорости К’ относительно К.

(2) r(V;V) = 0 - скорость тела, движущегося со скоростью V относительно системы К', движущейся с той же скоростью, равна нулю.

(3) r(r(v;V);-V) = v
(3.1) Если v параллельна V, то r(v;V) = - r(V;v)

«Сложение скоростей» можно определить как отношение:
(3.2) s(v;V) = r(v;-V)
Это определение следует из тождества (3).

И далее Фейгенбаум изучает свойства отношения "сложения скоростей" s(v;V) и доказывает, что это отношение НЕ является в общем случае ни ассоциативным, ни коммутативным. А именно:
s(v,v') = R(v';v) * s(v';v) - отношение коммутативно, только если "вращение" R=1
s(s(U;V);W) = s(R(-W;V)*U; s(V;W)) - отношение ассоциативно, только если выполняется R(-W;V)*U = 1.

Эти свойства операции "сложения скоростей" выводятся из принципа относительности Галилея и изотропии пространства.

Далее Фейгенбаум доказывает, что принцип относительности Галилея выполняется, если координаты и время в системе К и К’ связаны линейным преобразованием.

Принцип относительности Галилея: если тело движется с постоянной скоростью в системе К, то физически эквивалентными будут такие системы отсчёта, в которых это тело движется также с какой-то постоянной скоростью.
Если x = v * t + ksi - движение с постоянной скоростью v в системе К, то
x' = r(v;V) * t' + a(ksi;v) - движение с постоянной скоростью r(v;V) в системе К', которая движется со скоростью V относительно К.
Полагая, что
x' = f(x;t) и t' = g(x;t), Фейгенбаум доказывает, что эти функции линейные.
Факт линейности следует из того, что соотношение:
f(v*t+ksi; t) = r(v; V) * g(ksi + v*t; t) + a(ksi; v) - которое выражает условие, выделяющее физически-эквивалентные "миры Галилея" (в которых факт равномерности движения тел сохраняется), это соотношение должно выполняться при любых v; ksi; t.
А это можно обеспечить лишь для линейных функций x' = f(x;t) и t' = g(x;t).

Фейгенбаум отмечает, что преобразование Галилея – это частный случай общего линейного преобразования. Если же рассмотреть общий случай, то вместо преобразований Галилея:
x' = x - V * t
t' = t

Необходимо рассмотреть общее линейное преобразование:
(4) t’ = G(V) * (t – b(V) * x)
(5) x’ = G(V) * (L * x – A * t)

Здесь G(V) – число, зависящее от скорости V системы К’ относительно К, b(V) – некоторый вектор, А – тоже вектор, L – тензор.

Скорость точки в системе К’ равна:
(6) r(v;V) = v’ = x’ : t’ = (L * v – A ) : (1 – b(V) * v)

Учитывая свойства (1) – (2) получаем из (6):
(7) A = V
(8) L * V = V

Воспользуемся изотропией пространства. Пусть R – преобразование вращения. Тогда из (4) вытекает:
(9) t’ = G(R * V) * (t – b(R * V) * R * x)
Но с другой стороны, должно выполняться:
(10) t’ = G(V) * (t – (R * b(V)) * (R * x))

Сравнивая (9) и (10), получаем:
(11) G(R * V) = G(V)
(12) b(R * V) = R * b(V)

Отсюда следует, что функция G(V) зависит от V^2 – квадрата длины вектора скорости системы К', которая не меняется при вращениях.
Функция-вектор b(V), вследствие (12), имеет вид:
(13) b(V) = V : [C^2 (V^2)]

Инвариантная относительно вращений R константа обозначена как 1 : [С^2 (V^2)].

Учитывая (7) – (13), можно переписать (6) так:
(14) r(v;V) = (L * v – V) : [1 – (v * V) : C^2 (V^2)]

Если скорость тела v параллельна скорости системы К' (= V), то, учитывая (8), приводим (14) к виду:
(15) r(v;V) = (v – V) : [1 – (v * V) : C^2 (V^2)]

Учитывая (3.1), имеем:
(15.1) r(v;V) = - r(V;v) = (v – V) : [1 – (v * V) : C^2 (V^2)] = (v – V) : [1 – (v * V) : C^2 (v^2)]

Из (15.1) следует, что C^2 (V^2)] = C^2 (v^2)] при любом v.
Отсюда следует, что C^2 – это просто константа.

Таким образом, имеем окончательно:
(15) r(v;V) = (v – V) : [1 – (v * V) : C^2 ]

Учитывая определение "сложения скоростей" (3.2), находим
РЕЛЯТИВИСТСКИЙ закон сложения скоростей:
(16) s(v;V) = r(v;-V) = (v + V) : [1 + (v * V): C^2]

Таким образом, релятивистское правило сложения скоростей выводится без применения второго постулата Эйнштейна - принципа постоянства скорости света.
Преобразование Лоренца выводится из (4) и (5). Фейгенбаум показывает, как можно, шаг за шагом, получить все формулы СТО, используя лишь принцип изотропии пространства и принцип относительности Галилея.

Чтобы вывести «специальную теорию относительности» (СТО) постулат постоянства скорости света не нужен.

Это значит, что возможно, что скорость света не постоянна (если она меньше фундаментальной константы C). Формулы СТО – логически не зависят от постулата постоянства скорости света. Фейгенбаум пишет, что СТО можно было бы открыть ещё во времена Галилея. Всё, что для этого нужно, это – принцип равноправности равномерно движущихся относительно друг друга систем (принцип относительности Галилея) и изотропия пространства.

Фейгенбаум указывает причину возникновения релятивистских эффектов.
Он вводит определение параллельности пространственных осей систем K и K’. В системе К’ тоже можно ввести отношение параллельности с К’’.
Но из того, что К параллельна К’ и К’ параллельна К’’ НЕ СЛЕДУЕТ, что К параллельна К’’. То есть отношение параллельной ориентации пространственных осей не транзитивно.

Фейгенбаум указывает, что нетранзитивность есть следствие так называемых вращений Швингера. Аналитически эти "вращения" можно описать в виде соотношения:
(17) r(r(v;U); r(V;U)) = R(U;V) * r(v;V)

R(U;V) – вращение Швингера. Здесь r(v;V) – вектор скорости тела в системе K’, которую фиксирует наблюдатель системы К. Система К’ движется со скоростью V относительно К.
r(r(v;V’); r(V;V’)) - вектор скорости тела в системе K’, которую фиксирует наблюдатель системы К’’. Система К’’ движется относительно К со скоростью U. Эти два вектора скорости отличаются поворотом Швингера. На Рисунке схематически показано, как возникает такое вращение. Тело А кажется "повёрнутым", если за системой К' следить либо из системы К, либо из системы К''.



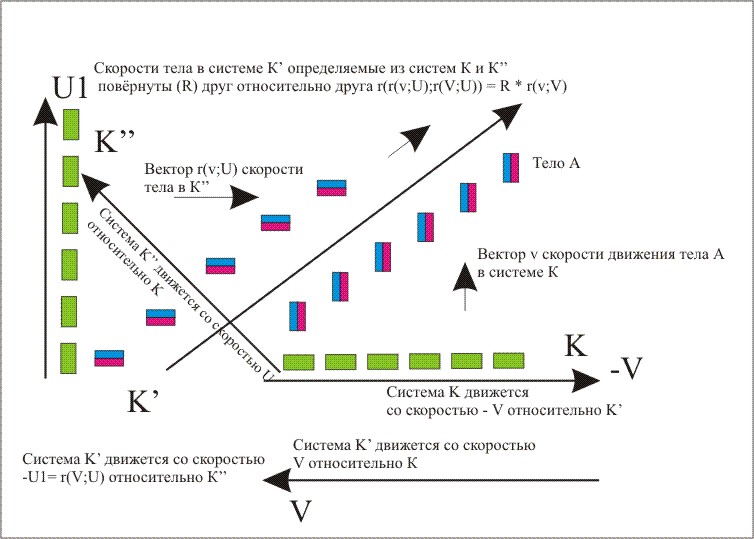
Рисунок воспроизводит поясняющий Рисунок из статьи:
NewScientist 29 October 2008 поместил статью
Mark Buchanon
Why Einstein was wrong about relativity (pp. 28-31)
где автор рассказывает об этом открытии.
http://www.newscientist.com/article/mg2 ... ivity.html

Предложенный Фейгенбаумом подход активно обсуждается с 2005 года.
Требуется солидная математическая подготовка, чтобы понять, что же такое эти "вращения Вигнера". Рисунок выше, хотя иллюстрирует суть проблемы, но, на наш взгляд, всё-таки не даёт полной картины и служит лишь наглядной иллюстрацией возникновения "специфических вращений": тело-прямоугольник при этом поворачивается вдоль оси, перпендикулярной плоскости скоростей.

Ясно только, что подход Фейгенбаума кардинально меняет всё наше понимание того, что такое релятивистские эффекты. Фундаментальная константа, стоящая в релятивистских формулах не обязательно равна скорости света. Только опыт может определить её значение. Если скорость света меньше этой константы, то фотоны должны иметь массу и, как любые массивные частицы, испытывать гравитационное притяжение, что, возможно, объясняет явление искривления лучей вблизи массивных тел.

К сожалению, в рунете не удаётся найти детальное описание Релятивистской Теории Фейгенбаума (РТФ). В то же время вопрос этот - причина релятивистских эффектов - настолько важен, что представляется необходимым обратить особое внимание на это новое понимание теории относительности (ТО).

Статья Фейгенбаума содержит результаты многолетних размышлений. Начиная с 2005 года Фейгенбаум сделал несколько выступлений на специальных встречах и семинарах, посвящённых новой трактовке ТО. Цитированная выше статья прошла двойное рецензирование. Фейгенбаум - учёный с мировым именем, автор теории универсальности режима приближения к хаосу. Уже поэтому его пересмотр логических оснований ТО - опубликованный после нескольких лет обсуждения этой теории в узком кругу специалистов - заслуживает самого глубокого изучения и анализа.

Статья поражает глубиной понимания проблемы и изяществом математических доказательств. Чтобы как следует вникнуть в суть предлагаемого Фейгенбаумом пересмотра ТО, эту статью надо читать много раз, возвращаясь снова и снова к началу, когда уже понятно, что будет в конце. Смысл фраз раскрывается не сразу, потому что содержит в себе огромный опыт проработки проблемы, вбирая осмысление уже полученных результатов.

Фейгенбаум пишет, что зная скорость системы К' относительно меня (скорость V) и скорость тела относительно меня (скорость v), Я могу задать вопрос: какой будет скорость тела относительно K'. Это будет какая-то вполне определённая скорость, вычисляемая по какому-то ПРАВИЛУ-1, которое зависит от v и V. Он обозначает это ПРАВИЛО-1 как r(v;V) и называет его "вычитанием" скоростей, в отличие от "сложения" скоростей, которое обозначается как s(v;V). Но, говорит Фейгенбаум, на самом деле ПРАВИЛО "сложения" сложением не является, поскольку не выполняются необходимые свойства операции сложения: коммутативность и ассоциативность. Фейгенбаум указывает, что в силу нарушения ассоциативности, правило "сложения" не является даже групповой операцией.

Фейгенбаум пишет, что у ПРАВИЛА-1 ("вычитание") r(v;V) есть свойство, которое НЕ БЫЛО ЗАМЕЧЕНО никем прежде. Это - инвариантность относительно вращений вокруг оси, перпендикулярной к плоскости скоростей v и V.

Он рассуждает так.
Представьте себе, - говорит Фейгенбаум, - что Вы - удалённый наблюдатель, который видит, что тело движется со скоростью v и что есть другая система отсчета K' (движущийся Галилеев мир), которая движется со скоростью V. Вы имеете ПРАВИЛО-1 r(.,.) , которое позволяет вам находить скорость тела в движущейся системе К', зная v и V. Согласно этому ПРАВИЛУ-1, вы строите вектор скорости v' = r(v;V).
Но что будет, если вы повернётесь, если система координатных осей, относительно которых вы фиксировали свои три вектора: v; V; r(v,V) - повернётся.

Меняет ли поворот ПРАВИЛО-1? Зависит ли ПРАВИЛО-1 вычисления скорости в системе K' от положения осей? Нет - говорит Фейгенбаум, - физика (а ПРАВИЛО - это физика) не меняется от поворота системы координат. В этом - суть изотропии пространства. Если пространство изотропно, то ПРАВИЛО-1 не изменится.
Но при повороте все три вектора v; V; r(v,V) - поворачиваются:
v1 = R*v
V1 = R*V
v'1 = R*v'

Применив ПРАВИЛО-1 к повёрнутым векторам v1 и V1, мы должны получить вектор v'1. То есть должно выполняться соотношение:
(24) r(R*v; R*V) = R*r(v; V)

Именно это свойство (24), выражающее инвариантность ПРАВИЛА r(.;.) относительно вращений, было не замечено ни Лоренцем, ни Пуанкаре, ни Эйнштейном. Свойство (24) накладывает определённые ограничения на возможный выбор ПРАВИЛА r(.;.), что и приводит, в конечном счёте, к релятивистским соотношениям.

Фейгенбаум пишет, что ПРАВИЛО-1 r(v;V) является осмысленным и однозначным алгоритмом лишь в том случае, если между системами К и K' установлено согласование ОСЕЙ пространственных координат.

Необходимо какое-то ПРАВИЛО-2, которое задаёт это согласование пространственных осей. ПРАВИЛО-2 позволяет связать два Галилеевых мира. Каждому направлению в одном мире К' соответствует определённое направление в другом мире К. Если, например, система пространственных осей в К' поворачивается, то ТОЧНО ТАКОЙ ЖЕ ПОВОРОТ происходит и в системе пространственных осей K. Поэтому один раз задав ПРАВИЛО-2 согласования направлений осей в К и К', можно считать два Галилеевых мира согласованными в смысле однозначности соответствия направлений.
Фейгенбаум предлагает в качестве ПРАВИЛА-2 использовать "параллельность". Согласованность направлений в К и К' означает тогда, что оси (x;y;z) в системе К соответственно параллельны осям (x';y';z') системы К'. Фейгенбаум подробно объясняет, что означает "параллельность" осей. Чтобы согласовать направления, ось OX системы К направляется вдоль вектора скорости системы К'. В системе К' за ось OX' выбирается направление противоположное скорости движения К относительно K'. Оси Ox и OX' - согласованы. Далее в системе К' выбирается произвольно ось OY' направленная перпендикулярно к оси OX'. На эту ось ставятся маркеры. Каждый такой маркер вычерчивает прямую линию в К. Множество таких линий в К определяет плоскость и ось OY выбирается как прямая в этой плоскости, перпендикулярная OX (направление OY определяется вращением против часовой стрелки от положительного направления OX к положительному направлению OY). Оси OY и OY' согласованы. Наконец, оси OZ и OZ' выбираются в обоих системах по правилу правого винта.

После того, как направления пространственных осей обоих систем согласованы, допустимы любые совместные вращения. При таких вращениях ПО ОПРЕДЕЛЕНИЮ согласованность направлений не нарушается. Введённая таким способом операция "параллелизма" однако не является транзитивной. Если мы согласуем оси систем К и К' по правилу-2, а потом оси К' и К'' по этому же правилу-2, то в общем случае оси систем К и К'' уже не будут согласованы. Если К'' - система, связанная с движущимся телом, то согласование направлений К и К' - необходимое условие для того, чтобы придать осмысленность и однозначность ПРАВИЛУ-1 r(v;V). Это - очень важный пункт. Чтобы иметь право писать r(v;V) как формулировку определённого однозначного и осмысленного ПРАВИЛА-1 нахождения скорости тела в системе К', движущейся со скоростью V относительно К, между системами К и К' должно быть установлено согласование пространственных осей по правилу-2.
Обозначение r(v;V) означает правило определения вектора скорости тела, которое движется со скоростью v относительно К - в системе К' которая сама движется относительно К со скоростью V ПРИ УСЛОВИИ СОГЛАСОВАННОСТИ направлений пространственных осей К и К'.
Но то же самое тело имеет какую-то другую скорость u, а система К' имеет какую-то другую скорость U - В СИСТЕМЕ К'', которая движется со скоростью V' относительно К.

Принцип относительности Галилея постулирует физическую равноправность всех равномерно движущихся друг относительно друга систем. Но это значит, что ПРАВИЛО-1 будет работать в каждой такой системе. Поэтому наблюдатель в системе К'' ТОЖЕ может воспользоваться этим правилом-1, чтобы определить скорость тела относительно К'. Он определит тогда, что эта скорость равна r(u;U). Но по тому же правилу-1 можно записать: u = r(v;V') и U = r(V;V') - скорость тела и системы К' относительно К''.

Фейгенбаум задаёт вопрос - а будет ли скорость тела относительно К' , найденная через применение правила-1 в системе К, совпадать со скоростью тела относительно К', найденной через применение правила-1 в системе К''? И отвечает - НЕТ в общем случае. Ведь при вычислении в системе К мы применяем согласование осей К и К', тогда как при вычислении в системе К'' мы применяем согласование осей К'' и К'. А это - разные согласования, поэтому и результирующая скорость тела в К' будет разной.

Математически это значит, что
r(r(v;V'); r(V;V')) НЕ РАВНО r(v;V).

Далее, Фейгенбаум говорит, что эти два вектора должны иметь одинаковую длину и могут поэтому лишь быть повёрнуты друг относительно друга. Поскольку - аргументирует Фейгенбаум, - величина скорости относительно некоторой системы К' - это всё-таки величина вполне определённая. Она не может зависеть от того, из какой системы она вычисляется. С величиной скорости связаны физические явления: передача энергии и импульса. Но физика не должна зависеть от того, из какой системы она описывается. Поэтому:
МОДУЛЬ(r(r(v;V'); r(V;V'))) = МОДУЛЬ(r(v;V))

А раз модули векторов равны, значит они отличаются лишь вращением и поэтому можно записать:
(9) r(r(v;V'); r(V;V')) = R(V';V) * r(v;V).
где R(V';V) - "вращение Вигнера". Если скорости V и V' параллельны или одна из равна нулю, то R = 1. Фейгенбаум пишет, что именно этот частный случай, как правило, рассматривается во всех учебниках по ТО - случай параллельности скоростей двух систем К' и К". И поскольку для этого частного случая самое важное - "вращение Вигнера" упускается из виду, то приходится дополнительно вводить второй постулат - постоянство скорости света. Если же с самого начал рассматривать задачу в общем виде, то все релятивистские соотношения можно вывести не прибегая к помощи второго постулата.

Именно формула (9) совместно с формулой (24) после аналитических преобразований позволяет вывести все эффекты специальной теории относительности.

Причины релятивистских эффектов заложены (1) в условии инвариантности ПРАВИЛА-1 относительно вращений в пространстве (24) и (2) в условии (9) неизменности физики (а значит модуля относительной скорости тела в определённой системе) вне зависимости от того, из какого Галилеева мира эта физика наблюдается (физическая равноправность миров Галилея).

Картинка выше, которая воспроизводит (с дополнительными пояснениями) Рисунок из журнала NewScientist, на мой взгляд, не вполне выражает то, что говорит в своей статье Фейгенбаум.

Для Фейгенбаума всякая попытка определить скорость тела относительно движущейся системы отсчёта связана с согласованием пространственных осей. Процедура такого согласования описана выше. Но такое согласование, пишет Фейгенбаум, ведёт к "поляризации" пространства - к выделению особого направления - своего для каждой движущейся системы. Это - направление скорости движения этой системы. Отношение r(v;V) неявно включает в себя операцию согласования осей. Этот символ означает: (1) мы рассматриваем систему K', которая движется относительно нас со скоростью V, (2) мы согласуем оси координат нашей системы с осями координат этой движущейся системы и в построенной таким образом координатной системе определяем значение скорости тела относительно K'. Потом мы рассматриваем ту же систему К', но уже из системы К", которая сама движется относительно нас со скоростью V'. Но в системе К" должно работать ТО ЖЕ САМОЕ ПРАВИЛО-1. То есть в ней скорость тела относительно К' определяется ТЕМ ЖЕ алгоритмом: то есть опять уже в системе К" мы согласуем оси системы К" с осями системы К' и в этой системе определяем вектор r(v';V') где v' и V' - скорости тела и системы К' в системе К". Но ясно, что во втором случае система согласованных осей, относительно которых определяется скорость тела в К', будет в общем случае ПОВЁРНУТА относительно системы осей в первом случае. То есть в результате такого правила определения скорости тела в К' мы обнаруживаем, что эта скорость будет вектором, который будет поворачиваться, а угол поворота будет зависеть от скоростей V и V'.

Ниже приведены Рисунки, иллюстрирующие, как возникает "вращение Вигнера" вектора скорости тела в системе К' при определении этой скорости посредством ПРАВИЛА-1 применённого в системах К и К''.





Из этих Рисунков видно, что хотя "абсолютное" положение вектора скорости не меняется (стрелочка направлена вверх в обоих случаях), направление этой стрелки относительно К' МЕНЯЕТСЯ.
ПРАВИЛО-1 - это рецепт, конструктивный алгоритм, который говорит, что надо сделать, чтобы получить скорость тела в системе К'. В силу физической эквивалентности всех равномерно движущихся систем этот алгоритм работает в каждой системе. Но вектора скорости тела относительно К', найденные по этому алгоритму, будут повёрнуты друг относительно друга в общем случае. Это вращение, связанное с процедурой согласования направлений осей, Фейгенбаум идентифицировал как "вращение Вигнера".
Можно было бы возразить, сказав, что надо лишь повернуть оси так, чтобы новые координаты вектора скорости не изменились. Но тогда ПРАВИЛО-1 не будет инвариантом относительно выбора системы отсчёта, из которой наблюдается движение тела относительно системы К'. А принцип Галилея в трактовке Фейгенбаума означает, что ПРАВИЛО-1 - формулируется универсальным путём - через согласование осей - их направлением вдоль вектора скорости системы К'. Поэтому направление осей определяется однозначно. Мы не имеем никакой возможности как-то совместить оси K' согласованные с К с осями К', согласованными с К''. Само это "согласование", опирающееся на параллелизм осей не является транзитивным. Поэтому оси К и К" никак не соотнесены между собой. Мы имеем два равноправных, но оторванных друг от друга МИРА, в каждом из которых работают одинаковые физические законы и применимо универсальное ПРАВИЛО-1, позволяющее находить скорость тел относительно движущихся систем.

Какое отношение данная Тема имеет к настоящему Форуму?

Идея Фейгенбаума по-моему гораздо глубже, чем технические аспекты теории относительности. Фейгенбаум утверждает идентичность законов Мира во всех мирах Галилея. Это в частности означает идентичность методов калькуляции относительной скорости объектов относительно движущихся в этих Мирах систем. Именно тот факт, что алгоритм определения скорости объекта относительно движущейся системы - должен быть ОДИН И ТОТ ЖЕ во всех мирах Галилей - именно этот факт вместе с условиями однородности и изотропности пространства и времени - приводят к релятивистским соотношениям. Факт поразительный, но доказываемый с математической точностью в статье Фейгенбаума. Этот результат снимает с повестки дня много лет длившиеся споры - верна ли теория относительности или нет.
Фейгенбаум говорит - да верна, но скорость, которая стоит в преобразованиях Лоренца вовсе не обязательно должна совпадать со скоростью света. Физика всех галилеевых Миров - абсолютно одинакова. То есть абсолютного движения нет. Его невозможно обнаружить. Но это не значит, что скорость света от источника движущейся системы будет такой же и относительно системы покоящегося наблюдателя. В этом смысле ненулевой результат опытов определения разности скоростей света в покоящейся и движущейся системах не является аргументом против СТО, а свидетельствует, что предельная скорость в преобразованиях Лоренца, видимо, отличается от скорости света.

Принцип физической эквивалентности Миров Галилея, если этот принцип распространить на АЛГОРИТМЫ, ведёт к глубокому пересмотру нашего понимания реальности. Физическая эквивалентность означает тогда, что Мир состоит из множества замкнутых на себя Миров, в каждом из которых работают одни и те же алгоритмы описания происходящего. Например, один из таких алгоритмов - это алгоритм определения скорости объекта относительно движущейся системы. Поскольку он работает во всех Мирах Галилея, чтобы это стало возможно, необходимы определённые взаимоотношения между измеряемыми в разных мирах пространственными отрезками и временными промежутками. Причём оказывается, что эти соотношения не могут быть другими кроме как преобразованиями Лоренца. Псевдоевклидова геометрическая структура возникает как условие согласования результатов применения одинаковых алгоритмов в разных мирах.

Но это свойство можно обобщить. Можно предположить, что не только СТО, но и ряд других "законов" возможно является не чем иным как правилами согласования применения некоторых универсальных алгоритмов, одинаковых во всех физически идентичных Мирах. Физически-идентичные Миры, привязанные к Наблюдателям, напоминают монадологию Лейбница. Возможно концепция "общего мира", в который как в сосуд погружены наблюдатели, не соответствует реальности. А то, что мы обычно связываем с понятием "общий мир" - совокупность правил согласования универсальных алгоритмов, работающих внутри каждого Мира. Одно из таких правил создаёт иллюзию псевдоевклидова "общего пространства". Потому, возможно, и кажется, что свойства СТО противоречат здравому смыслу, что мы пытаемся объективировать эти свойства, тогда как они лишь правила согласования результатов действия универсальных алгоритмов. То, что есть на самом деле - это Мир каждого отдельного наблюдателя и правила упорядочения информации в этом каждом отдельном Мире. Эти правила упорядочивания (алгоритмы) не противоречат друг другу, если результаты упорядочивания некоторым образом согласованы ("предустановленная гармония" Лейбница). И только когда мы приписываем правилам согласования объективность - мы этим выносим их вовне и наделяем их самостоятельностью - так возникает "объективная реальность", которая вполне может оказаться фикцией. Объективно же реальными могут оказаться именно все отдельные замкнутые в себе Миры ("монады").
Это гипотеза. Но такая гипотеза в принципе возможна.

Логическая структура квантовой механики как обобщение подхода Фейгенбаума.

Принцип физической эквивалентности миров Галилея можно обобщить, встав на позиции множественности миров (приняв концепцию Лейбница). В этом случае внутри каждого мира можно задать алгоритмы обработки информации - операции, применяемые к "объектам" мира и дающие в результате действия числа (измеряемые или наблюдаемые величины). Согласованность применения алгоритмов в разных мирах наделяет определённой структурой результаты применения алгоритмов и через это устанавливает определённую алгебру (или математическую структуру) для самих алгоритмов (операций).

Можно попытаться взглянуть с этой точки зрения на логическую структуру квантовой механики (КМ). Операторы в КМ в такой интерпретации описывают алгоритмы, а состояния задают "объекты". Числа же (измеряемые величины) должны зависеть как от "объекта", так и от той "системы отсчёта", относительно которой состояние объекта изучается. В теории Фейгенбаума если v скорость тела и V скорость системы отсчёта, то r(v;V) - скорость тела относительно этой движущейся системы отсчёта. Отношение r(v;V) можно рассматривать как частный случай алгоритма, который использует информацию о состояниях движения тела (v) и системы отсчёта (V). Если мы хотим этот способ описания обобщить, нам понадобится ТРИ параметра - изучаемый объект, та система, в которой этот объект будет отражён и то, что отражается. Например, нас интересует импульс тела в системе, которая как-то представлена в нашем мире. Мы можем сказать, что эта система, относительно которой мы будем определять импульс тела, имеет в нашем мире состояние a. Мы можем далее сказать, что состояние объекта в нашем мире - это состояние b. И что мы хотим узнать, каким будет значение импульса объекта в этой системе. Алгоритм, который определяет состояние импульса, обозначим Р. В результате аналогично тому как мы писали r(v;V) мы теперь пишем:
(*) (b|P|a) - измеряемый импульс объекта, который имеет состояние b в нашем мире относительно системы А, которая имеет состояние a в нашем мире. Здесь P - алгоритм определения импульса.

Теперь точно так же, как это в работе Фейгенбаума, мы можем применить ТОТ ЖЕ алгоритм, но уже в системе, которая имеет состояние с в нашем мире и записать:
(b1|P|a1), где а1 - состояние системы А в мире С и b1 - состояние объекта в мире С.
Если мы теперь введём операции перехода из нашего мира в мир С - например, обозначив U - то будем иметь:
b1 = b|U и a1 = U*|a
Мы должны отличать "левое" и "правое" положения состояния внутри отношения (*). Поэтому и при описании перехода из мира А в мир С надо ввести два алгоритма U и U*.

Если результаты применения алгоритмов в А и в С - одинаковы, то это значит что миры А и С физически эквивалентны. Обозначив R - алгоритм определения РЕЗУЛЬТАТА действия алгоритма Р в А и С, получим:
R[(b1|P|a1)] = R[(b|UPU*|a)] = R[(b|P|a)]

Поскольку это соотношение должно выполняться при любых b; a; P получаем:
UPU* = Р

Возможно, двигаясь таким путём, можно попытаться осмыслить КМ как концепцию связи (согласования) результатов применения одинаковых алгоритмов в разных мирах. Если такое понимание допустимо и согласовано с КМ, то СТО и КМ объединяются в рамках одной схемы и выражают физическую эквивалентность всех миров.

Здравствуйте, Григорий.
Честно говоря, рассуждения Фейгенбаума представляются слишком отвлечёнными. Что это за такая загадочная скорость в преобразованиях Лоренца ? Эксперименты показывают (и практика покалывает), что это именно скорость света, а не что-либо иное.

С однородностью и изотропностью пространства связаны, как известно, законы сохранения импульса и момент импульса сооответственно. А тут появляется ещё какая-то загадочная скорость с совершенно неясным физическим смыслом.

И вообще, это действительно тот самый Фейгенбаум ?

И по поводу лично Ваших рассуждений, Григорий. Под состоянием Вы имеете здесь в виду именно то, что обычно и обозначается этим словом в КМ, или всё-таки несколько иное ?

Здравствуйте, Artashir.



Да. "Тот самый Фейгенбаум".
http://en.wikipedia.org/wiki/Mitchell_Feigenbaum

Сейчас он работает в Институте Рокфеллера.
http://www.rockefeller.edu/graduate/fac ... .php?id=38

Статья действительно сложная и требуются серьёзные усилия, чтобы понять логику рассуждений. Но вывод однозначен - преобразования Лоренца могут быть выведены без привлечения второго постулата Эйнштейна. При этом в преобразованиях появляется некоторая константа, имеющая размерность скорости. Но само значение этой константы можно определить лишь опытным путём. Она может совпадать со скоростью света, если опыт это покажет, но может и отличаться.

Споры о результатах опытов Майкельсона и других учёных не утихают до сих пор. Действительно ли скорость света постоянна (второй постулат) или нет - вопрос этот по-прежнему не имеет общепризнанного ответа. Есть учёные, которые считают, что результат опытов Майкельсона по обнаружению "эфирного ветра" показывают этот эффект, хотя он гораздо слабее, чем ожидалось. Если считать, что фундаментальная скорость, стоящая в преобразованиях Лоренца - это скорость света, то "эфирный ветер" должен отсутствовать, если же предположить, что скорость света немного меньше фундаментальной скорости, то "эфирный ветер" будет, но гораздо слабее, чем это следует из классических представлений. Но именно такой слабый эффект и показывают опыты Майкельсона. Это можно трактовать как свидетельство отличия фундаментальной скорости от скорости света.

Фейгенбаум при выводе использует 1) свойства однородности и изотропности пространства и 2) постулат единственности (одинаковости) алгоритма определения скорости тела относительно движущейся системы отсчёта. Именно одинаковость этого алгоритма во ВСЕХ системах лежит в основе "Вигнеровского вращения" вектора скорости относительно движущейся системы, определяемого из разных "миров Галилея" (из разных систем отсчёта).

Ещё раз. Есть множество "миров Галилея" - движущихся равномерно друг относительно друга систем отсчёта. И есть некоторая система, относительно которой мы хотим определить скорость тела. Во всех "мирах Галилея" действие этого алгоритма одинаково - вследствие физической эквивалентности этих миров. Но применяя этот алгоритм из разных миров, получим вектора, повёрнутые друг относительно друга. Это вместе со свойствами алгоритма и условиями изотропности и однородности приводит к преобразованиям Лоренца.

Теория очень красивая и глубокая. По-моему, Фейгенбаум прав.

Григорий.

"Слабый эфирный ветер" как следствие отличия фундаментальной константы в преобразованиях Лоренца от скорости света.

В теории Фейгенбаума фундаментальная константа с размерностью скорости, стоящая в формулах преобразования координат и времени, измеряемых в разных Галилеевых мирах, не обязательно должна совпадать со скоростью света. Формально вид преобразований совпадает с преобразованиями Лоренца. Отличие в том, что вместо скорости света стоит некоторая фундаментальная константа с размерностью скорости. Лишь опыт должен показать, чему эта константа равна. Если она равна скорости света, то выполняется второй постулат Эйнштейна. В этом случае "эфирный ветер" отсутствует. Но если фундаментальная константа больше скорости света, должен наблюдаться "слабый эфирный ветер".

Возьмём формулу сложения скоростей при сонаправленном движении тела и движущейся системы отсчёта:
(1) v = (V + v') / (1 + v * v'/C^2)

Здесь: v - скорость тела относительно лабораторной системы отсчёта,
V - скорость движущейся системы отсчёта,
v' - скорость тела относительно движущейся системы отсчёта,
C - фундаментальная константа.

Пусть свет движется относительно "эфира" со скоростью c и пусть лабораторная система движется со скоростью -V относительно "эфира". То есть система, связанная с "эфиром", движется со скоростью V относительно лабораторной системы. Тогда v' = с - скорость света относительно "эфира". Подставив в (1), получаем:
(2) с1 = (V + c) / (1 + c * V/C^2) - скорость света, относительно лабораторной системы.

При противонаправленном движении пучка света и системы отсчёта "эфира" (относительно наблюдателя) получим для ВЕЛИЧИНЫ скорости света в лабораторной системе:
(3) с2 = (с - V) / (1 - c * V/C^2)

Модуль разности этих скоростей определяет максимум разности скоростей двух пучков света, движущихся по и против "эфирного ветра".

Составив разность delta = (с1 - с2):c после несложных преобразований находим:
(4) delta = [2 * beta * gamma * (gamma - 1)] : [gamma^2 - beta^2]

Здесь:
beta = V : c
gamma = (C:c)^2

Из формулы (4) видно, что разность скоростей двух пучков света, движущихся "по" и "против" направления "эфирного ветра" равна нулю только если gamma =1 - то есть когда фундаментальная константа совпадает со скоростью света. Если же скорость света меньше фундаментальной константы, то будет наблюдаться "эфирный ветер", который однако тем "слабее", чем меньше отличие значения скорости света от значения фундаментальной константы.

Наблюдаемое изменение скорости может при этом быть очень малым.
Интересно, что опыты Майкельсона дали НЕ-нулевой результат, хотя значительно меньший, чем ожидалось. На эту тему:
http://n-t.ru/tp/ng/sev.htm




Если взять в качестве V орбитальную скорость Земли, то наблюдаемый эффект "эфирного ветра" в 3 км/сек соответствовал величине delta = 1/10 beta [ (c2 - c1):c = 3 : 300 000 = (1/10) * 30 : 300 000 = V : c). При этом величина gamma = (C:c)^2 примерно равна 20/19. То есть С примерно в 1,026 больше скорости света.

То есть, приняв теорию Фейгенбаума в принципе можно объяснить, почему наблюдаемый "эфирный ветер" в опытах Майкельсона оказался намного слабее, чем это ожидалось. Настолько "слабым", что в большинстве практических задач можно считать его нулевым и пользоваться обычной релятивистской теорией, считая, что скорость света постоянна.

Многие физики приводят аргументы в пользу отказа от второго постулата Эйнштейна и модификации СТО.

http://www.network54.com/Forum/304711/t ... RELATIVITY

Обнаружено, что нейтрино двигаются со скоростью большей скорости света.
http://ru.euronews.net/2011/11/18/new-t ... -s-theory/
http://www.youtube.com/watch?v=uFEa1ykm19I

С точки зрения "теории Фейгенбаума" в этом нет ничего особенного. Если в преобразованиях Лоренца стоящая там фундаментальная константа немного больше скорости света, то нейтрино вполне могут двигаться со скоростью большей скорости света. Если эта фундаментальная константа лишь немного превышает скорость света, то в системах отсчёта, движущихся относительно друг друга, скорость света будет почти одинакова.

Берём релятивистскую формулу сложения скоростей:
(1) v = (v' + u)/(1+v'u/c0^2)
здесь v' - скорость тела в системе отсчёта, которая движется со скоростью u относительно лабораторной системы отсчёта, v - скорость тела в лабораторной системе отсчёта, с0 - фундаментальная константа, имеющая размерность скорости.
В теории относительности эту фундаментальную константу отождествляют со скоростью света. В теории Фейгенбаума с0 - это не обязательно так.

Итак пусть с0 немного больше скорости света: с0 > с. Положим: c0 - c = d. Пусть v' = c. Имеем:
(2) v = (c + u)/(1+cu/c0^2)

Составим разность:
(3) v - c = u : [1 + c(c+u)/{d(2c+d)}]

Возьмём, например, следующие значения:
c0 = 300010 км/с
с = 300000 км/с
u = 12 км/с - чуть больше второй космической скорости.

v - c = 0.0008 км/с = 80 см/с

Отклонение порядка погрешности измерения скорости света в наиболее точных опытах

http://bse.sci-lib.com/article102991.html

Таким образом, скорость света, если она мало отличается от фундаментальной константы с0, не одинакова в разных системах отсчёта, но отличие будет настолько мало, что оно лежит в пределах точности измерения этой величины. То есть наблюдатели, которые будут измерять скорость света - один на Земле, а другой - на космическом корабле, мчащемся со второй космической скоростью, получат значения, которые будут одинаковы в рамках погрешности измерений. Наблюдатели могут сделать вывод, что скорость света не зависит от движения системы отсчёта, что она - фундаментальная константа, но на самом деле, это не обязательно так. В силу близости скорости света к истинной фундаментальной константе с0 значения скорости света в разных системах отсчёта отличаются настолько мало, что это различие очень сложно обнаружить.

Опыты с нейтрино можно рассматривать как подтверждение, что фундаментальная константа больше скорости света, то есть теория Фейгенбаума верна.
Поскольку все релятивистские соотношения при этом сохраняются (надо лишь заменить с на с0), то теория относительности этими опытами опровергнута быть не может.

Что должно измениться?
Во-первых, придётся признать, что фотон (квант света) имеет массу покоя, как и нейтрино, поскольку нулевая масса покоя может быть лишь у частицы, которая движется с фундаментальной скоростью с0.
Во-вторых, это означает, что существуют системы отсчёта, в которых фотоны покоятся - свет не движется. То есть двигаясь вдоль луча лазера со скоростью света, которая должна быть достижима (ведь нейтрино движутся даже быстрее света) мы "увидим" застывший свет, неподвижный относительно движущейся системы отсчёта.
В-третьих, уравнения Максвелла уже не будут инвариантны относительно преобразований Лоренца, в которых произведена замена скорости с на фундаментальную константу с0.

Новая интерпретация ТО.

Наши физики тоже пришли к тем же выводам, которые получил Фейгенбаум: теорию относительности можно вывести без постулата постоянства скорости света. Полученные в новой интерпретации ТО преобразования координат и времени от одной системы отсчёта к другой по форме совпадают с преобразованиями Лоренца, но вместо скорости света содержат фундаментальную константу с размерностью скорости. Опыт должен показать, равна эта константа скорости света или больше скорости света. Недавнее открытие, что нейтрино могут двигаться со скоростью большей скорости света, по-видимому, указывает, что фундаментальная константа всё же больше скорости света.

Русские авторы новой интерпретации ТО:
Манида Сергей Николаевич (СПбГУ, физфак).
Преобразования Лоренца. Глава 2 - Вывод преобразований Лоренца из принципа относительности //Лекции для школьников. Библиотека Физического факультета СПбГУ, URL: http://www.phys.spbu.ru/library/schooll ... r/chapter2

Степанов Сергей Сергеевич, Релятивистский мир, URL: http://synset.com/ru/%D0%9F%D1%80%D0%B5 ... 1%86%D0%B0

===========================================================================================================
Путенихин Пётр Васильевич сопоставляет традиционный подход и новый и правильно пишет, что если константа в преобразования Лоренца больше скорости света, то меняется очень многое в том, к чему мы успели привыкнуть.
http://quantmagic.narod.ru/volumes/VOL912012/p1146.html

Он пишет:


То есть альтернативная трактовка ТО ведёт к необходимости глубокого пересмотра некоторых физических идей, к которым мы все привыкли. Возможно, физикам всё же удастся как-то иначе объяснить аномальную скорость нейтрино, не нарушая при этом традиционную ТО. Если же не удастся, то придётся пересмотреть некоторые устоявшиеся воззрения.

Что-то никак не удаётся поставить точку в более чем на век затянувшемся недоразумении с мировым эфиром. Действительно, опыт Майкельсона-Морли показал, что движение вещественных объектов (и связанных с ними систем отсчёта (СО)), никак нельзя примирить с очевидным, казалось бы, распространением света по субстанции эфира. Решение научного сообщества, с подачи Эйнштейна, было прямо скажем парадоксальным - эфир был признан «несуществующим». То, что сим актом из мироздания изгонялась, можно сказать, материальная его основа, почему-то было признано приемлемым. В результате физические поля стали не состоянием их носителя эфира, а самостоятельными сущностями, характеризуемыми рядом параметров, и только.

На смену физическим моделям мироздания пришли умозрительные математические конструкции, а построение физической картины мира из принципов однородности и изотропности пространства, из принципа относительности физических процессов, очаровало многих физиков. Вообще-то достаточно сложная математическая теория может описать что угодно, например как теория струн или торсионных полей. Не исключение и теория Фейгенбаума.
А вот существование эфира как как бы грозит разрушить эту гармонию, так как появляется выделенная абсолютная система отсчёта. Однако многие физики считали, что вещество должно иметь «первооснову», на роль которой разумеется предлагался эфир. Построено множество эфирных теорий: эфиродинамика, ритмодинамика, баллистическая теория и пр. Но у всех эфирных теорий возникает проблема совместимости с СТО - всё тот же опыт Майкельсона. Поэтому серьёзные учёные их даже не рассматривают.

Основная проблема эфирной теории состоит в объяснении причин Лоренцева сокращения движущихся тел и замедления в них времени. Без него у эфира нет преимуществ по сравнению с постулатом ПСС. Ещё Лоренц указывал, что если признать эти два (строго говоря достаточно первого) феномена за факт, то все формулы СТО выводятся элементарно. Однако разумных объяснений возможных причин сих феноменов не последовало, и, согласно махистскому принципу «экономии мысли», был принят постулат постоянства скорости света (ПСС) и построена соответственная ему математика пространства Минковского, в которой обеспечивается инвариантность 4-х мерного интервала событий относительно преобразований группы вращений. Сиё нисколько не объяснило природу феномена, но сделало бессмысленным сам вопрос. Следует отметить, что фигурирующий там параметр “C” теперь уже не какая-то скорость света, а является мировой константой. Совпадение её значения со скоростью света в теории не объясняется.

Эфирная теория, о выводах из которой рассказывается ниже, математически обоснована в статье на сайте http://cardiac.narod.ru/index/ether2/0-19#h00/ .

Эфир и вещество. Давайте вспомним, какой эфир предлагался к согласованию с опытом Майкельсона. В нём вещество (атомы, частицы) двигались внутри эфира, однако состояли из иной, отличной от эфира «вещественной» субстанции. Такой эфир действительно несовместим с опытом Майкельсона и не существует.
Но представим эфир, который составляет основу вещества - т.е. из которого построены частицы и всё сущее. Но как это может быть? Если предположить, что эфир состоит из маленьких «апейрончиков», а уже из них лепятся частицы, то мы просто переводим проблему на уровень ниже, но не снимаем её.
Значит следует предположить, что частицы и вообще вещество - это состояние эфира представленное напряжениями и деформациями эфирной субстанции. Напряжения свойственны именно твёрдым и упругим телам, поэтому будем считать, что эфир твёрдый и упругий. А вещество (частицы) представлено "картинкой" напряжений и деформаций, «нарисованной» в эфирной субстанции.
В таком случае все силовые взаимодействия «материальных» картинок и их перемещения в толще эфира определяются взаимодействием силовых полей в эфире. Целостность «вещественной частицы» обусловлена тем, что эфирная картинка суперпозиций амплитуд и фаз, образующих её силовых полей, остаётся относительно неизменной как в покое, так и при движении частицы.

Итак, почему же движущиеся тела сокращаются по Лоренцу? Когда картина суперпозиций, изображающая частицу, начинает двигаться, то взаимодействия от её заднего фронта, передаваемые по эфиру с некоей скоростью распространения, начнут запаздывать, так как им придётся двигаться вдогонку. А взаимодействия от переднего фронта наоборот, будут набегать быстрее, так как двигаются навстречу. Обмен взаимодействиями между двумя точками тела частицы состоит в том, что воздействие от первой достигает второй, и поучившееся там новое состояние распространяется снова к первой - и так же наоборот. Таким образом, акт взаимодействия пары точек состоит из обмена волновыми «посылками» «туда» и «обратно».
Следовательно, волновая суперпозиция полей тела частицы сохранит устойчивость, если времена взаимодействия пар точек, которые были одинаковы в покое, при движении «волнового пакета» тоже останутся одинаковыми, хотя численно станут другими.
Не сложный расчёт показывает, что для этого волновой пакет частицы должен сжаться по Лоренцу, а время взаимодействия при этом будет аналогично увеличено. Таким образом, при движении в эфире каждая частица и весь их ансамбль РЕАЛЬНО сжимаются, а времена процессов в них РЕАЛЬНО замедляются.
Можно показать, что преобразования Лоренца в этом случае остаются справедливыми. Поэтому ни в какой системе отсчёта локальными экспериментами не удастся обнаружить её движение относительно Эфира. Феномен постоянства скорости света теперь является следствием и уже не постулат. А параметр “C” теперь является скоростью распространения силовых полей в эфире. Он больше не константа, так как скорость передачи взаимодействий зависит от состояния эфира в каждой точке и может изменяться со временем.

Но раз тела при ускорении и увеличении скорости сжимаются, значит сжимается и тот объём эфира, который они ранее занимали. Соответственно на сжатие упругого эфира должна быть затрачена энергия. Это должна быть как раз та энергия, которая затрачена на ускорение тела. Если предположить, что энергия сжатия эфира пропорциональна степени его сжатия (обратно пропорционально объёму), то можно показать, что энергия сжатия эфира представляет собой то, что мы называем массой тела, и затем вывести известное E = «эм це квадрат». Из равенства энергии, затраченной на ускорение тела и посчитанной по правилам Ньютоновой механики, и энергии пошедшей на сжатие эфира, можно вывести уравнения динамики, которые окажутся совпадающими с такими же релятивистскими в СТО.

Разумные предположения (математического и экспериментального обоснования пока не имеют).
Естественно, может возникнуть вопрос об устойчивости волновых пакетов соответствующих частицам. Известно, что колебания и волны не склонны создавать устойчивые образования. А линейно-упругие свойства эфира будут способствовать нивелированию всяких перенапряжений.
Но если при превышении некого порога напряжений у эфира проявляются нелинейные свойства, то там где такое случилось, могут появиться устойчивые образования - нечто типа «чёрных микродыр». Правда и для дальнейшего их существования тоже нужно приложение внешних сил. Более подробно этот сценарий рассматривается на сайте http://cardiac.narod.ru/index/ether3/0-26 и там же высказаны некоторые соображения о природе электрических зарядов, магнитных полей и причинах гравитации. Ну и вообще об эволюции вселенной.

Здравствуйте, А. П.

Интересный материал Вы цитируете.
Насколько я понял, основная идея автора состоит в том, что любые две точки тела взаимодействуют (обмениваются световыми сигналами) за одно и то же время T. Автор пишет:


Это как-то странно. Если две ПАРЫ точек находятся на разных расстояниях (например, точки 1 и 2 на расстоянии 1 см, а точки 3 и 4 на расстоянии 10 см), то как они могут взаимодействовать (обмениваться световыми сигналами) за одинаковое время? Этот пункт требует дополнительных пояснений.

С уважением,
Григорий.

Действительно там так и написано - никогда не обращал внимания. Я думаю, здесь несколько неудачно пытались донести мысль, что времена взаимодействий 1-й точки со 2-й (туда-сюда) и 2-й с 1-й (сюда-туда) должны быть одинаковы. Разумеется если имеем 2 пары разнодистантных точек, то времена будут разные, но изменятся равно пропорционально. Важно, что группы пар точек, которые в покое взаимодействовали за равное время, и при движении должны взаимодействовать тоже за равные времена - как-то так.