С О Ц И Н Т Е Г Р У М

C Методом Системного Потенциала (МСП) можно ознакомиться в разделе "Публикации" нашего форума (на русском языке).

МСП - это метод моделирования Сложных Адаптивных Систем (САС).
http://en.wikipedia.org/wiki/Complex_adaptive_system
http://www.google.com/url?sa=t&source=w ... WA&cad=rja

САС - это система, состоящая из множества взаимодействующих агентов, каждый из которых пытается достичь максимального "выигрыша". Взаимодействия агентов могут быть прямыми или через среду их общего обитания. Поведение агентов регулируется "схемами", которые аккумулируют их индивидуальный опыт и в рамках этого опыта обеспечивают им наилучший выбор из выделенных ими альтернатив. Такое поведение позволяет агентам адаптироваться в меняющейся ситуации.
1) САС - это сложная система, которая может вести себя непредсказуемо и нелинейно. Даже небольшие изменения "входных данных" или "внешних воздействий" могут вызвать глубокие качественные и часто неожиданные изменения в устройстве и поведении САС.
2) САС - это адаптивная система, состоящая из множества агентов, которые пытаются приспособиться к окружающей среде и найти в ней свою нишу.

Можно назвать САС ансамблем взаимодействующих адаптивных агентов. Реальные САС окружают нас повсюду. Мы сами являемся Сложными Адаптивными биологическими (живыми) Системами. Каждый из нас включён во множество социальных и экономических САС, внутри которых он выполняет определённые функции. Классическими примерами САС являются рынки - рынки товаров и рынки капиталов (фондовые рынки). Ещё во время войны стало ясно, что знание об устройстве и принципах работы сложных систем несёт огромные преимущества тем, кто этим знанием владеет. Возникшая после войны "системная динамика" (Форрестер) была первым шагом в понимании того, что такое сложные системы, как они устроены и развиваются.
http://www.google.com/url?sa=t&source=w ... Nw&cad=rja

Существенный шаг вперёд был сделан после появления мощных компьютеров, которые можно стало использовать для моделирования реальных САС. Создание виртуальных миров, населённых виртуальными агентами, ведущими себя в соответствии с определёнными правилами адаптивного поведения позволило впервые начать систематическое изучение моделей поведения многоагентных систем приближенных к реальности. Стало возможно визуально посмотреть, что будет с тем или иным виртуальным миром в том или ином случае при том или ином его устройстве при тех или иных правилах поведения агентов. Многоагентное моделирование (МАМ) стало мощным инструментом познания свойств реальных САС. МАМ позволила выявлять свойства системы как целого в ходе "проигрывания" соответствующей многоагентной модели на компьютере. В течение последних 20 лет накапливалось знание, полученное изучением поведения разных многоагентных моделей. Не сразу, но мало по малу с течением времени становилось ясно, что такие МАМ-модели, часто совершенно не схожие в своём устройстве и моделирующие совершенно разные реальные САС, тем не менее ведут себя в некотором смысле сходным образом, то есть показывают одинаковые макроскопические закономерности (см. ниже). МСП - это попытка понять, почему РАЗНЫЕ МАМ-модели демонстрируют ОДИНАКОВЫЕ макроскопические свойства. Почему, например, все приближенные к реальности МАМ-модели развиваются в режиме "прерывистого равновесия" или почему в них эпизодически происходят быстрые качественные изменения в структурном устройстве (реконфигурации), почему "масштаб" таких качественных изменений системы (большие качественные, малые качественные изменения), если взять статистику, будет случайной величиной с обратно-степенным законом распределения.... Понять закономерное происхождение этих (и многих других) макроскопических свойств САС можно, по-видимому, исходя из каких-то общих фундаментальных законов развития таких систем. Возникает мысль связать эти универсальные макроскопические свойства САС с законами эволюции, которые действуют на уровне всей системы как целого. Эта идея лежит в основе нового метода моделирования САС - Метода Системного Потенциала (МСП).

МСП - это способ моделирования Сложных Адаптивных Систем (САС) по принципу "сверху-вниз", от законов развития целостной системы к законам динамики ее составляющих.
Законы развития САС как целостных систем опираются на принципы эволюции, предложенные Ламарком (законы Ламарка). САС - это ансамбль агентов, способных осуществлять адаптивный поиск (адаптивные агенты) через процессы накопления опыта, обучения и изменения своих программ поведения (включая мутации). Такие ансамбли в реальном мире составляют огромное множество реальных САС. Это - организмы (ансамбли взаимодействующих клеток-агентов), социо-экономические системы, крупные организации, экосистемы, страны, города, регионы, фондовые и финансовые рынки, системы распределенных сетей, объединяющих в одно целое множество операторов (например, энергосети). Традиционно для моделирования таких систем применяется Много-Агентное Моделирование (МАМ-платформа). После появления мощных компьютеров стало возможно создавать виртуальные миры - сложные системы взаимодействующих виртуальных агентов. После длительного опыта накопления информации о поведении таких виртуальных САС, стало ясно, что все они, несмотря на существенно разное строение и конкретные особенности поведения агентов, показывают один и тот же набор универсальных макроскопических свойств:
(1) режим прерывистого равновесия,
(2) циклическую динамику макропоказателей,
(3) сложное соединение детерминистической и стохастической составляющих,
(4) фрактальные свойства структуры и свойство самоподобия динамики макроиндексов,
(5) эпизодические внезапные реконфигурации - катастрофы,
(6) явление самоорганизованной критичности,
(7) явление самоорганизованной нестабильности...

Традиционная платформа МАМ - опирается на принципы эволюции Дарвина (адаптивный поиск агентов есть не что иное как "борьба за выживание" Дарвина). Наиболее приближенные к реальности виртуальные модели САС, выстроенные на основе МАМ платформы модели, демонстрируют вышеперечисленные свойства.

Эти свойства невозможно "вывести" из свойств принципов, заложенных в поведение агентов и их взаимодействий. Такие неожиданные свойства сложных систем, невыводимые из поведения агентов, называют эмерджентными свойствами САС (emergent properties). Эти свойства демонстрируют очень разные МАМ модели (имеющие разное строение и разные правила адаптивного поиска) - поэтому их можно называть универсальными свойствами.

МСП, опираясь на формализацию законов эволюции Ламарка, предлагает объяснение этих универсальных эмерджентных свойств и дает их математическую теорию. МСП дополняет традиционный "снизу-вверх" ("bottom-up" - от поведения агентов к эмерджентным свойствам САС) подход, используемый МАМ. Подобно тому как в физике ансамбль взаимодействующих молекул как целое, может быть описан методами "термодинамики", с использованием макровеличин, задающих макроскопическое состояние вещества (давление, температура, энропия, внутренняя энергия и т.д.) - точно так же ансамбль взаимодействующих адаптивных агентов как целое может быть описан посредством "термодинамических" характеристик этого ансамбля - таких понятий как:
(1) "адаптивный потенциал" САС - аггрегированная способность системы к адекватному ответу на внутренние и внешние угрозы,
(2) "условия, от которых зависит, какая часть имеющегося адаптивного потенциала" применяется системой в данный момент,
(3) "реализуемый потенциал" - та часть адаптивного потенциала, которая применяется.
(4) Отношение применяемой части адаптивного потенциала к полной его величине характеризующая "эффективность" процесса адаптации (поиска наиболее оптимального и быстрого ответа на возникающие угрозы).
(5) Отношение количества "условий" к величине "потенциала" ( = "оснащенность САС"), характеризующее обеспеченность системы необходимыми для нормального развития условиями реализации ее потенциала.

Развитие САС на макроскопическом уровне регулируется законами Ламарка.
ПЕРВЫЙ ЗАКОН ЛАМАРКА:
Та часть адаптивного потенциала, которая применяется в текущей деятельности системы - растет. Примеры действия этого закона - рост применяемых способностей в результате тренинга и обучения.

ВТОРОЙ ЗАКОН ЛАМАРКА:
Неиспользуемый в текущей деятельности адаптивный потенциал постепенно дегенерирует. Примеры действия этого закона - отмирание неиспользуемых способностей организма, дисквалификация, например.

ТРЕТИЙ ЗАКОН ЛАМАРКА.
Система в очень длительном периоде (охватывающем много эволюционных циклов) стремится найти такую конфигурацию, в рамках которой процесс адаптации протекал бы наиболее эффективно. Такая конфигурация предполагает некоторое оптимальное соотношение между разными составляющими САС: между ее разными подсистемами и уровнями организации. Это - свойство поиска ГАРМОНИИ или СОВЕРШЕНСТВА. Ламарк писал о стремлении всех живых организмов к внутреннему совершенству.

Кроме этих трех законов, МСП постулирует существование двух стабилизирующих механизмов:
Первая стабилизирующая обратная связь описывает процесс стабилизации текущего временного макроскопического состояния САС как целостной системы. Стабилизирующая обратная связь обеспечивает возвращение системы в ее состояние текущего равновесия в случае отклонений, вызванных действием возмущающих факторов. Примерами действия этого закона являются процессы гомеостаза в организмах или, если в качестве примера взать экономическую САС - процессы регуляции типа Вальраса и Маршалла (так называемый Walrasian-Marshallian adjustment).

Вторая стабилизирующая обратная связь описывает способность САС перераспределять агентов между ячейками структуры так, чтобы этим обеспечивать максимальную эффективность адаптации системы как ансамбля взаимодействующих агентов. Этот механизм приводит к созданию многоуровневой структуры с фрактало-подобными свойствами. Примером действия этого мехнизма является возникновение классов в обществе, иерархий в животных сообществах...

Две петли обратной связи лежат в основе макроскопической динамики САС:
1) возбуждающая положительная обратная связь: "накопленный опыт" (потенциал и условия реализации) - адаптивная деятельность системы - прирост в накопленном опыте - "reinforcing feedback process".
2) регулирующая отрицательная обратная связь: отклонение от равновесия - действие первой и (или) второй стабилизирующей обратной связи - возвращение во временное равновесное состояние.

Эти законы описывают МАКРО-эволюцию, тогда как взаимодействие отдельных агентов внутри САС подчиняется законам борьбы за выживание, то есть регулируется законами Дарвина.
МИКРО-эволюция осуществляется по законам Дарвина. МАКРО-эволюция совершается по законам Ламарка и черз процессы поддержания текущего макроскопического равновесного состояния.

Оба плана эволюционного развития глубоко взаимосвязаны между собой. Можно сказать, что законы эволюции Ламарка "эмерджентны" по отношению к законам эволюции Дарвина. Агенты, конкурируя между собой за источники выживания и развития в этой совместной борьбе за существование создают на уровне САС как целостной системы - тенденции развития в соответствии с законами эволюции Ламарка.
Длящиеся много лет споры о соотношении микро и макро эволюции, о соотношении законов Дарвина и законов Ламарка - находят свое разрешение в рамках системного подхода.

МСП формализует действие законов Ламарка и указывает путь, двигаясь по которому можно связать в единое целое оба плана эволюции.

БОЛЕЕ ПОДРОБНО С ОСНОВНЫМИ ПОЛОЖЕНИЯМИ МСП можно ознакомиться в Разделе "Публикации" Форума.
Представленные там работы написаны на русском языке.
Наиболее понятной и доступной для широкого читателя будет статья:
"Метод Системного Потенциала и Эволюционные Циклы".

Статья: "Динамика Системы как Процесс реализации ее Потенциала" написана в 2003 для Международной Конференции по Системной Динамике. В тот момент МСП активно разрабатывался, и многие положения еще не были четко сформулированы. Эта статья имеет одно преимущество - оно содержит общий анализ МСП-Систем, параметры которых могут быть переменными. Здесь же рассматриваются принципы классификации возможных способов развития систем.

Статьи "О применении МСП...", "Модель бизнес-цикла..." и "Динамика в коротком и длинном периодах" были подготовлены для Конференции, организованной Международным Институтом имени А. Богданова. Некоторые выводы последней статьи были позже пересмотрены.

С точки зрения философии, МСП можно рассматривать как попытку формализовать некоторые фундаментальные аспекты мироздания - его строения и развития.
Многие известные философы - Платон, Спиноза, Лейбниц, Гегель, Спенсер, Бергсон... - на абстрактно-логическом языке, используя философскую терминологию, формулировали эмерджентные свойства САС.

1) Спиноза ввел понятие "субстанции" как причина самой себя (causa sui). В рамках концепции САС, "субстанция" - это фундаментальная обратная связь, лежащая в основе свойства целостности системы:
свойства агентов (и их взаимодействия) - эмерджентные свойства системы - эффект индуцирования (перенесения) эмерджентных свойств системы на уровень отдельных агентов - новые свойства агентов....
Agent-agent interactions - emergence - immergence - new type of agent-agent interactions...

Фундаментальная петля через звенья: "emergence" (от агентов к целостной системе) - "immergence" (от целостной системы к отдельным агентам) замыкает каждого агента на самого себя, создавая "монадный" эффект - эффект замкнутого на себя мира.

2) Этот аспект САС - "монадология" был развит в работах Лейбница. Он рассматривал Универсум как множество монад - замкнутых миров. Лейбниц высказал две фундаментальных догадки:
(1) идею фрактальности строоения Мироздания. Эту идею он выражает как идентичность принципов построения и действия монад разных размеров и масштабов. По Лейбницу "большие монады" вроде человеческого организма состоят из множества более мелких, которые в свою очередь состоят из еще более мелких. В результате структурные особенности монадного строения простираются как вглубь так и вширь, создавая - как мы сейчас назвали бы это - фрактальную структуру Универсума.
(2) Вторая идея Лейбница - его учение о "предустановленной гармонии". Ей соответствует а) идея согласования всех масштабов организации через потоки фундаментальных петель обратной связи (многомасштабная субстанциальность) и б) идея "потенциального бытия", которую позднее подробно разрабатывали Шеллинг и Гегель.

3) Гегелевская диалектика - его учение о спирали развития, перидических качественных метаморфозах, о противоречиях как движущей силе развития - может быть ре-интерпретирована через применение концепции САС (в особенности - МСП). Иррегулярные разрывные циклы (cycles with discontinuites) - состоящие из двух фаз плавного изменения макро-величин и двух резких скачков, возникающих в результате математической катастрофы в развитии МСП-Системы, - формируют режим прерывистого равновесия (intermittent dynamics) и эпизодического качественного обновления строения САС (спираль развития через эпизодические реконфигурации - метаморфозы системы).

Ниже результаты моделирования динамики МСП-систем:

График 1. Циклы сжатия: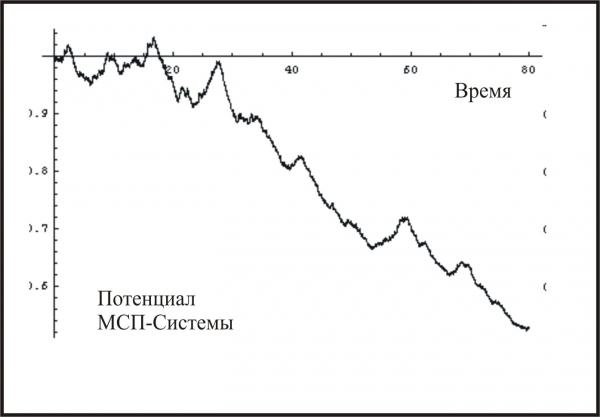



График 2. Циклы расширения.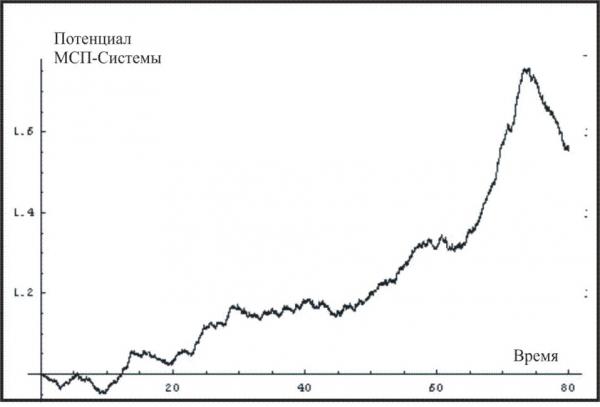



ВОЗМОЖНЫЕ ПРИМЕНЕНИЯ МСП.
1) В области управления реальными САС - в экономике, техническом анализе финансовых и фондовых рынков, в управлении разветвленными сетевыми структурами: корпорациями, системами государственного управления....
2) В области предсказания аварий и естественных катастроф - экологических катастроф, изменений климата, в гелиобиологии...
3) В теории реконфигураций САС - включая теорию эволюции (происхождения видов).
4) При разработке мер по обеспечению системной безопасности - созданию мониторинга вредных воздействий на систему и выработке мер по повышению эффективности использования адаптивного потенциала систем.
5) В науках, которые изучают "фундаментальную обратную связь" и ее возможные проявления: математическая диалектика, математическая экология, математическая экономика...
(Перечень далеко не полный)

МСП можно рассматривать как средство для разработки нового типа систем искусственного интеллекта, которые можно применять для гибкой самонастройки реальных САС. Такие болезненные явления современных обществ как "коррупция", "семейственность", "клановость", "паразитизм", "низкая эффективность", "рост бюрократии"... могут быть излечиваемы через применение технологий САС-МАМ-МСП при разработке новых законов и принципов управления страной.

Первое сообщение по МСП было в 2003 году.
С осени 2003 этот метод был включен в международный курс системной динамики на многих языках.

МСП может быть органично увязан с традиционным подходом - много-агентным моделированием (МАМ). Возможно создание МАМ-МСП платформы для изучения динамических и структурных свойств Сложных Адаптивных Систем (САС). Такая платформа может объединить в себе как "снизу-вверх" ('bottom-top") так и "сверху-вниз" ("top-bottom") методологии. Ее поэтому можно назвать " Bottom-Top-Bottom" (BTB) платформой моделирования САС.

ПРАКТИЧЕСКАЯ ПОЛЬЗА ОТ ИССЛЕДОВАНИЙ В ЭТОЙ ОБЛАСТИ.
(1) управление реальными сложными адаптивными системами: социальными, экономическими, социально-экономическими, экологическими, социально-экономико-экологическими, региональными, меж-страновыми....
(2) финансовые и фондовые рынки.
(3) оценка рисков и оптимизация портфеля инвесторов.
(4) диагностика состояния реальных САС и вероятностный прогноз их развития.
(5) разработка мероприятий по повышению уровня адаптивной гибкости САС.
(6) системная безопасность: создание новой дисциплины - обеспечение системной безопасности социо-экономических САС. Это - и повышение устойчивости к природным катаклизмам, и меры, направленные на снижение природных бедствий, и меры оценки взаимодействия с другими странами с точки зрения их влияния на процесс развития своей страны. Защита от разрушения собственного "потенциала".

Перечисленные выше ВЫГОДЫ позволяют поставить задачу создания теории управления реальными САС на базе МАМ-МСП платформы. Такую теорию управления логично назвать САС-Менеджмент. Это - совокупность определенных правил диагностики состояния реальных САС и рекомендаций, направленных на повышение уровня их адаптивной гибкости.

Мы назвали это - ПРОЕКТ САС-МЕНЕДЖМЕНТ (CAS-Management Project).
Уникальность этого Проекта - в разработке имеющих большую практическую ценность технологий управления сложными много-уровневыми сетевыми структурами, состоящими из множества взаимодействующих агентов. Такие организации генерируют так называемые "эмерджентные свойства" (непредсказуемые события макроскопического масштаба), примерами которых являются: коллапсы фондовых рынков, длительные депрессии в экономике, распады систем (например, распады империй), глубокие кризисы, реконфигурации (в социальных системах известные как "революции")... Эти "непредсказуемые" события, хотя их появление и нельзя точно предсказать, все же статистически подчинены определенным закономерностям, изучением которых и занимается САС-Менеджмент.

С идеями МСП можно ознакомиться также по материалам данного форума - в этой теме и в темах:
"Обзор работ, методологически близких МСП"
viewtopic.php?t=60

"Циклы российской цивилизации"
viewtopic.php?t=79

===================================================================================================================================
СПИСОК ЛИТЕРАТУРЫ ПО МСП (на английском):
(List of Publications:
Method of Systems Potential (MSP) as "top-bottom" approach in the Complex Adaptive Systems modelling.

Pushnoi, G. S. (2003). Dynamics of a system as a process of realization of its “potential”. Proceedings of the 21st International Conference of the System Dynamics Society, July 20-24, New York.
Paper # 205 in on-line directory: http://www.systemdynamics.org/conferenc ... ed/PAPERS/

Pushnoi, G. S., (2004a). Method of Systems Potential and Evolutionary Cycles. Working paper presented at inter-disciplinary scientific forum: viewtopic.php?f=14&t=10&start=0

Pushnoi, G. S., (2004b, November). Application of Method of Systems Potential for Analysis of Economic System Evolution. Paper presented at the Second Internet Conference on Evolutionary Economics and Econophysics. Ekaterinburg, Russia: International A. Bogdanov Institute.
English version: http://econpapers.repec.org/paper/wpawuwpdc/0505014.htm

Pushnoi, G. S., (2004c, November). The Business Cycle Model on the Basis of Method of Systems Potential. Paper presented at the Second Internet Conference on Evolutionary Economics and Econophysics. Ekaterinburg, Russia: International A. Bogdanov Institute.
English version: http://econpapers.repec.org/paper/wpawuwpdc/0505016.htm

Pushnoi, G. S., (2005, April). Long-term and short-term dynamics of the Economic System on the basis of Systems Potential Method. Paper presented at the Third Internet Conference on Evolutionary Economics and Econophysics. Ekaterinburg, Russia: International A. Bogdanov Institute.
English version: http://econpapers.repec.org/paper/wpawuwpdc/0506001.htm

Pushnoi, G. S., Bonser G. L. (2008). Method of Systems Potential as “Top-Bottom” Technique of the Complex Adaptive Systems Modelling. In Ang Yang & Yin Shan (eds.) Intelligent Complex Adaptive Systems, IGI-Publishing, Hershey-London, 26-73.
http://openlibrary.org/b/OL16921994M/In ... ve_systems

Pushnoi, G. S. (2010).Crisis as Reconfiguration of the Economic Complex Adaptive System. AAAI Simposium Series; AAAI Fall CAS Simposium; USA.
http://aaai.org/ocs/index.php/FSS/FSS10/paper/view/2234

Pushnoi, G. S. (2014). Method of System's Potential as Holistic Approach for CAS-Modelling. Chapter in Mehdi Khosrow-Pour (Ed.) "Encyclopedia of Information Science and Technology", Third Edition, chapter 707, pp. 7180-7191. IGI-Publishing, Hershey-London.
http://www.igi-global.com/book/encyclop ... hird/76156
http://www.igi-global.com/chapter/metho ... ing/112416

Pushnoi, G. S. (2017). Method of Systems Potential (MSP) Applications in Economics: Emerging Research and Opportunities. IGI-Publishing, Hershey-London.

https://www.igi-global.com/book/method- ... ons/172437

В июне 2017 выходит книга, в которой рассказывается - как можно использовать Метод Системного Потенциала для анализа макроскопической динамики экономической системы. В книге собран, дополнен и систематизирован материал, касающийся общих принципов этого Метода. Построена экономическая модель, основанная на принципах этого Метода. Показано, как можно применить Модель для практических расчётов макроэкономической динамики. Подробно рассмотрены два крупных кризиса: кризис начала 1930-х (Великая Депрессия) и кризис 2008-2009 годов. Рассмотрена динамика производительности труда в Европейском Союзе с 1950 по 2014 годы. Показано, что созданная на основе принципов МСП экономическая модель теоретически верно объясняет изменения в производительности труда в Евросоюзе в этом периоде. Соответствие теории и фактических данных достаточно высокое (коэффициент детерминации > 0.99). В последней главе книги рассмотрено обобщение Метода Системного Потенциала для систем с переменными параметрами и применение Модели для анализа экономики США. Дано объяснение причины кризиса 2009 года на основе МСП-модели с переменными параметрами. Хотя в книге много математических выкладок и расчётов, основные выводы выделены отдельно и обильно иллюстрированы графиками и рисунками. Поэтому для понимания основных результатов не обязательно детальное знание математических нюансов.

Книга предназначена для специалистов в области экономического моделирования, сложных и сложных адаптивных систем, теоретиков макроэкономики, специалистов в области теорий циклического развития экономики. Книга будет полезна для практиков в области управления экономикой и прогнозирования макроэкономических процессов и для специалистов по финансовым и фондовым рынкам.
http://www.igi-global.com/book/method-s ... ons/172437

Grigorii S. Pushnoi.
=======================================================================

ДОБАВЛЕНИЕ.
Дата: 25 Октября 2010.

Метод Системного Потенциала (МСП) дополняет традиционно применяемое сейчас (при моделировании САС) многоагентное моделирование (МАМ).

МСП объясняет происхождение ряда универсальных макроскопических свойств САС, обнаруженных в последние 20 лет при изучении поведения многоагентных САС-моделей:
(1) поведение большинства моделей показывает режим «прерывистого равновесия» - стадии плавного развития системы перемежаются внезапными резкими скачками, которые сопровождаются реконфигурацией САС,
(2) во многих моделях, приближенных к реальному прототипу, наблюдается наличие четырёхфазной циклической динамики (так называемые четырёхфазные разрывные циклы) изменения макроскопических показателей системы,
(3) многие модели показывают обратно-степенной закон распределения величин катастрофических событий в системе, (4) большинство моделей показывает свойство самоорганизованной критичности (self-organized criticality),
(5) и свойство самоорганизованной нестабильности (self-organized instability),
(6) а также фрактальные свойства иерархического древа и динамики макроиндексов САС.

МАМ (многоагентное моделирование) описывает САС по принципу «снизу-вверх»: макроскопические закономерности здесь возникают как непредсказуемый агрегированный эффект взаимодействия множества относительно автономных агентов, стремящихся достичь своих целей (максимизировать свой выигрыш, безопасность, приспособленность…).

МСП описывает САС по принципу «сверху-вниз». Одинаковость (у многих разных МАМ-моделей) перечисленных выше макроскопических свойств САС указывает на существование общей причины, которая лежит в их основе. МСП постулирует несколько простых эволюционных принципов, которые объясняют происхождение этих макроскопических свойств САС. Эволюционные принципы МСП восходят к эволюционным идеям Ламарка, тогда как МАМ моделирует поведение агентов, в основном опираясь на эволюционные принципы Дарвина.

Соотношение между МАМ и МСП моделированием аналогично соотношению статистического и термодинамического подходов в современной физике. Макроскопические переменные МСП («потенциал системы», «условия для реализации этого потенциала», «эффективность выполнения задач адаптации») описывают свойства и динамику САС как целостной системы и играют роль «термодинамических потенциалов» для ансамбля взаимодействующих агентов, - подобно тому, как макроскопические переменные «температура, давление и др.» описывают поведение и свойства (как целого) ансамбля взаимодействующих молекул.

Согласно МСП, развитие САС в длинном периоде может протекать разными способами - иметь тренд деградации, застоя или прогресса в зависимости от значений параметров САС. МСП даёт строгую математическую формулировку этим свойствам долговременной динамики САС и позволяет оценивать возможности развития системы по тому или иному пути.

САС-методология сейчас активно используется на Западе для принятия управленческих решений в самых разных областях практической жизни людей – в администрировании, политике, экономике, экологии, военном деле, медицине…

МСП, применённый к экономической САС, приводит к новой модели, объясняющей циклическое развитие и эпизодически происходящие катастрофы (кризисы) рыночной экономики. Проверка МСП на данных Роберта Солоу о развитии обрабатывающей промышленности США в первой половине 20 века, подтверждает основные выводы экономической МСП-модели и даёт новое объяснение феномену «великой депрессии». Собранные недавно данные Paolo Giussani о закономерностях соотношений между производительностью труда, капитала и фондовооружённостью в экономиках 100 стран мира за последние 50 лет тоже находят объяснение в рамках МСП-модели.

МСП может быть использован:
1) при создании новых систем искусственного интеллекта,
2) для снижения рисков принятия решений в ситуациях, когда объект управления сложен и ведёт себя нелинейно и часто непредсказуемо,
3) для анализа устойчивости конкретных САС и повышения их адаптивных свойств,
4) при прогнозировании риска нежелательных неожиданных событий – катастроф разного масштаба, возникающих вследствие высокой неустойчивости внутри определённых частей и звеньев системы к тем или иным воздействиям,
5) для повышения степени защиты САС к неблагоприятным внешним воздействиям.

МСП можно использовать в создании практических приложений в экономике, менеджменте, экологии, военном деле, строительстве, маркетинге, политике, медицине…

Создание новых систем виртуальной реальности, опирающихся на МСП-МАМ платформу моделирования, позволит максимально приблизить виртуальные модели к их реальным прототипам, что даст странам (разработавшим такие виртуальные системы) огромные конкурентные преимущества в новом 21 веке.

Такие САС-модели виртуальных миров дают странам, освоившим эту технологию, возможность просчитывать возможные последствия принимаемых решений и выбирать оптимальные процедуры принятия решений. Например, прежде, чем проводить какую-то реформу, её можно «проиграть» на компьютере, оценив все плюсы и минусы и выбрать оптимальный вариант, тем самым сэкономив средства и минимизировав возможные потери. Такие виртуальные модели уже создаются на Западе для изучения и регулирования финансовых рынков, экономики, в области военного строительства.
==================================================================================================================

P.S. (от 03.10.2014) Я удалил часть материала, который содержал описание возможных применений "МСП" и ссылки на статьи, авторы которых пытаются применять "МСП" в разных областях системного анализа. Писать дальше ради заполнения пустого пространства не вижу смысла. Если появится интерес - пишите на E-mail:
gpushnoi@yahoo.com


Григорий Сергеевич.

Прочитал статью на
http://www.inauka.ru/blogs/article49193.html
Возникли следующие вопросы:
1) Что Вы называете оснащённостью ? Из текста статьи это неясно.
2) О каких шести вариантах развития систем идёт речь ?

Здравствуйте, Artashir.
"Оснащенностью" я называю отношение величины "условий" к величине "потенциала", то есть количество "условий", приходящихся на единичный "потенциал".

"Вариант развития" определяется знаками производных по времени от трех величин: "потенциала", "условий" и "оснащенности" - всего 8 комбинаций. Однако две из них невозможны вследствие определения термина "оснащенность". Если "потенциал" растет, а "условия" убывают, то "оснащенность" может только уменьшаться. И другой вариант - убывание "потенциала" и рост "условий" означают рост "оснащенности". Поэтому только 6 вариантов возможны.

Спасибо за ответ. Григорий.

Как понять "слабо флюктуирующие". Кто их должен флюктуировать ?

Следует ли понимать это так, что имеет место катастрофа ? Вы говорите о том,
что это области джокера. Но область джокера - это когда малое воздействие
ведёт к непредсказуемым изменениям. Можно ли понимать под воздействием
изменение констант уравнений a; d; b и m ?
И вот здесь мне не вполне понятно: что такое
?

Здравствуйте, Artashir.

Спасибо большое за ответ.

1. О флюктуациях и их происхождении.

Эволюционные параметры любой реальной системы, то есть величины a, d, b и m не являются математическими константами. Это - случайные величины, средние значения которых в течение определенных интервалов времени меняются незначительно. Если дисперсии этих случайных величин малы, то внутри таких интервалов времени система развивается так как если бы значения эволюционных параметров были почти постоянными величинами.

Положение точек z0 и z1 зависит от значений эволюционных параметров. Поэтому малые отклонения мгновенных значений этих параметров от среднего приводят к малым смещениям точек z0 и z1 по отношению к положениям этих точек, определяемым средними значениями эволюционных параметров в рассматриваемом периоде. Эти мгновенные случайные смещения точек z0 и z1 малы, если малы дисперсии эволюционных параметров. Именно такие случайные малые смещения точек z0 и z1 относительно средних значений этих величин я и называю флюктуациями. Флюктуация случайной величины мала, если отношение дисперсии к среднему значению этой величины много меньше единицы.
Флюктуации эволюционных параметров отражают наличие множества случайных факторов в эволюции реальных систем.

2. О катастрофе и "джокере".

В окрестности точек z0 и z1 происходит скачок системы с одной эволюционной ветви на другую. Это именно катастрофа в математическом смысле этого слова. Термин "джокер" был введен Георгием Геннадьевичем Малинецким, в первую очередь, для фиксации стадии непредсказумого резкого изменения состояния системы. По Малинецкому эволюцию систем можно представить как чередование фаз плавного детерменированного развития внутри определенного "русла" и фаз резкого скачкообразного изменения состояния системы - "джокеров". Отличительная черта "джокера" - непредсказуемость результата.

Скачки системы с одной ветви на другую есть та фаза эволюции систем, которую, если сравнить наш Метод с концепцией "русла" - "джокер", следует отнести к фазе "джокера". Скачки эти возникают в областях неустойчивого положения системы - в окрестности точек z0 и z1. Под действием флюктуации точек z0 и z1 система покидает область устойчивости и совершает скачок с одной ветви на другую. Стадия скачка не описывается эволюционными уравнениями Метода Системного Потенциала. Поведение системы во время скачка детерменировано лишь в смысле направления с одной эволюционной ветви на другую. В каком месте новой эволюционной ветви окажется система после скачка - на этот вопрос нельзя ответить точно. Скачок может произойти либо вертикально, либо под некоторым углом. Кроме того, в фазе кризиса, то есть в фазе падения системы с верхней на нижнюю эволюционную ветвь, часто происходит мутация системы, то есть изменение значений эволюционных параметров. Мутация же сопровождается изменением кривой R(z). Предсказать мутацию невозможо. Мутации есть тот механизм, через который система развивается и совершенствуется - самоорганизуется, как теперь говорят. На стадиях скачков вверх - фаза восстановления после периода депрессии - происходит активное вовлечение в деятельность прежде бездействовавших пластов "потенциала". Этот процесс также плохо прогнозируем. Поэтому скачки с одной ветви на другую имеют свойства "джокеров".
Конечно, кроме скачков системы с одной ветви на другую система может переживать фазы "джокеров" других видов. Например, вследствие неожиданного резкого воздействия на систему: стихийное бедствие или "подарок судьбы" - система может совершить резкий скачок в плоскости "потенциал" - "условия". Эти скачки, вызванные значительным внешним воздействием на систему и зависящие от внешних случайных факторов, также можно расматривать как "джокеры".

Условия и потенциал системы могут меняться либо за счет деятельности системы, либо за счет притока или оттока этих величин через "границы" рассматриваемой системы с другими системами. Если пренебречь влиянием внешнего окружения на изменение потенциала и условий, то прирост этих величин регулируется исключительно деятельностью самой системы. Уравнения эволюции выведены именно на основе этого предположения. Однако, возможны ситуации, когда такое внешнее влияние нельзя не учитывать. Например, переезд из страны с низким уровнем жизни в страну с высоким уровнем жизни сопровождается резким скачком величины условий. Другие примеры - крупный выигрыш или землетрясение, разрушившее все, что человек создавал десятилетиями.

Григорий.

Григорий, это очень интересная модель. Скажите, как Вы её исследовали ? Проигрывали ли на компьютере ?
И ещё, учитывая, что

можно ли утвержать, что по математической форме модель состоит не просто из обыкновенных дифференциальных уравнений, а из стохастических дифференциальных уравнений. Иными словами, в Ваших уравнениях
a, d, b и m это всё-таки константы или случайные переменные ?
И как Вы моделируете упомянутые Вами мутации этих эволюционных параметров ?

Здравствуйте, Artashir.

Я рад, что Вы так оперативно отвечаете. Спасибо.

Модель, наверное, действительно интересная. Это признали и рецензенты той версии, которая была представлена на конференции. Я продолжаю над ней работать, когда выдается свободное время. К сожалению "условия реализации" моего "потенциала" оставляют желать лучшего, поэтому дело идет не так быстро, как хотелось бы.

О том, на какой стадии находится работа.
Возможно несколько стадий приближения Метода к реальности:
1) Положить, что значения эволюционных параметров есть постоянные величины. Это приводит к системе дифференциальных (не стохастических) уравнений для "потенциала", "условий", "оснащенности", "показателя эффективности системы". Получены точные аналитические решения. Зависимость "показателя эффективности" от "оснащенности" изображена на одном из рисунков, приложеных к статье.
2) Учесть существование малых флюктуаций эволюционных параметров. Это приводит к циклической динамике системы. Используя полученные на первой стадии исследования формулы, можно просчитать длительность разных фаз цикла и зависимость этих длительностей от величины флюктуаций. Можно составить также классификацию циклов, основанную на том, какие "варианты развития" проходит система, двигаясь по нижней и верхней ветвям цикла. Два вида цикла могут существовать лишь как "циклы расширения", в которых "потенциал" и "условия" прирастают после полного цикла. Остальные циклы могут существовать в трех возможных формах - как циклы "расширения", "сжатия" или в виде замкнутых циклов. Можно построить поверхность катастрофы системы - поверхность с острым "гребнем" типа "волны" и изучать динамику системы методами теории катастроф.
3) Более строгий подход требует, конечно, использования стохастических дифференциальных уравнений, поскольку параметры a, d, b и m являются случайными величинами. Более того, средние значения этих случайных величин могут быть функциями, например, от "оснащенности" системы. Здесь возможны самые разные ситуации и приближения.
4) Очень интересная тема - влияние внешних воздействий на эволюцию системы. Возможно два пути. Случайное внешнее воздействие и рассмотрение системы как подсистемы внутри некоторой другой, объемлющей. В первом случае - случайные скачки. Во втором случае обе системы - та, которая рассматривается и объемлющая ее более глобальная система - обе развиваются по одинаковым законам. Чтобы это могло иметь место между объемлющей системой и ее подсистемой должна возникнуть некоторая связь, которая выполняет роль условий согласования уравнений динамики обоих систем. Эта ситуация напоминает ту, которая имеет место в теории гравитации, где уравнения движения источников поля являются условиями совместного выполнения уравнений поля. Причина - в нелинейности уравнений поля. Эволюционные уравнения - тоже нелинейные уравнения.
5) Если рассмотреть ансамбль систем, равномерно распределенных в плоскости "потенциал" - "условия" в начальный момент времени, то с течением времени произойдет расслоение систем на несколько групп. Системы выстроятся вдоль линий конвергенции своих "областей развития". Этот процесс легко наблюдать на компьютере. Такое расслоение систем на несколько классов с разными значениями "оснащенности" возможно объясняет процесс стратификации общества на несколько слоев с разным средним уровнем дохода.

6) О моделировании флюктуаций и мутациях. Это очень специальные темы. Моделирование флюктуаций требует привлечения стохастических методов. Мутации могут быть случайными и закономерными. Закономерными я называю мутации, которые повышают уровень организации системы. Например, мутация экономической системы США после 1929 года была закономерна. Вопрос о мутационном процессе очень сложный. Мутации системы лежат в основе ее качественного усложнения. Поэтому я склоняюсь к той точке зрения, которую высказывает, например Alexei Sharov в своих статьях по семиодинамике - мутацию (выбор в точках бифуркации) нельзя рассматривать как исключительно случайный процесс. Существует "контроль" над выбором линии развития в ключевых бифуркационных точках эволюции системы. Наличие такой контролирующей процесс эволюции информации на уровне отдельного организма - совершенно очевиден. Я думаю, что и другие сложные адаптивные системы подобно living systems также мутируют по определенной программе. Во всяком случае мутация экономической системы США после 1929 года не была случайным событием. Необходимые аргументы для обоснования этой точки зрения я надеюсь представить в статье, посвященной описанию Великой Депрессии с позиций Метода Системного Потенциала.

С уважением, Григорий.

Итак, если я правильно понял, для исходных детерминированных уравнений, описанных в статье, аналитическим путём было получено непереодическое решение.
В случае же, если a, d, b и m - случайные переменные, то, как Вы полагаете, решение будет периодическим. В связи с этим у меня следующий вопрос: на чём Вы основываете последнее утверждение о цикличности решения ?

Здравствуйте Artashir.

Если эволюционные параметры абсолютные константы (чего в реальном мире не бывает), то циклической динамики не будет. Показатель эффективности будет асимптотически приближаться к максимально возможному значению, равному единице. "Оснащенность" при этом стремится к значению z0. Но это - совершенно нереальная ситуация.
Циклы возникают вследствие того, что в окрестности точек z0 на верхней эволюционной ветви и точки z1 на нижней эволюционной ветви положение системы перестает быть устойчивым. Потеря устойчивости и приводит к скачкам, которые могут быть стимулированы флюктуациями параметров системы.

Ситуация напоминает ту, которая встречается в теории нелинейных колебаний. В этой теории амплитудно частотная зависимость осциллятора имеет форму наклоненного "гребня". В теории доказывается, что в точках с вертикальными касательными к АЧЗ осциллятор находится в неустойчивом положении, в результате чего наблюдаются скачки амплитуды колебаний при плавном изменении частоты.

В нашем случае скачки в точках неустойчивого положения системы, z0 и z1, переводят систему с одной эволюционной ветви на другую и при этом характер монотонности функции z(t) меняется. Убывание z по нижней ветви после скачка в окрестности точки z1 сменяется ростом z по верхней ветви. В окрестности второй точки неустойчивого положения системы, z0, происходит падение системы на нижнюю ветвь, после чего цикл повторяется. Имеет место явление гистерезиса - поэтому я называю эти циклы гистерезисными эволюционными циклами.

Конечно, цикл возможен только если b>d.

Григорий

Судя по этому описанию видно, что Вы "чувствуете" уравнения, то есть исходя уже из математического вида уравнений оцениваете, как себя будут вести переменные при тех или иных дополнительных условиях.
Тем не менее, думаю, были бы интересны и численные решения этих уравнений, численные эксперименты с ними.

Здравствуйте, Artashir.

В статье, над которой я сейчас работаю, будут приведены все основные выкладки и будет дан анализ полученных математических выражений. Основные результаты будут иллюстрированы с помощью рисунков и графиков. Там же будут даны некоторые результаты численного моделирования на компьютере.

Спасибо за Ваш интерес к моей работе и Ваши замечания.
Григорий.

Вам спасибо за Ваши материалы. С интересом ознакомлюсь с Вашей будущей статьёй. Думаю, данная тематика стоит того, чтобы её разрабатывать дальше.

И ещё по поводу уравнений. Григорий, фактически Вы решали именно одно уравнение - Якоби, то есть уравнение R относительно Z, а не уравнения с исходными переменными F, Fr, U ?

Здравствуйте, Artashir.

Конечно, нет. Уравнения для функций U(t); F(t) и z(t) также решены. Просто размеры статьи не позволяют привести эти результаты. Величина Fr экспоненциально растет во время движения вдоль эволюционной ветви и меняется скачком во время фаз кризиса и восстановления. Это резкое изменение Fr связано с процессом перераспределения накопленного системой потенциала между реализуемой и нереализуемой частями. В фазе кризиса доля нереализуемой части потенциала резко возрастает, в фазе восстановления происходит обратный процесс - потенциал, если можно так выразиться, перетекает из резервуара нереализуемой части в резервуар реализуемой. Это приводит к скачкообразному изменению траектории Fr(t). В плоскости (F;U) фазам скачка соответствуют точки излома траектории (F(t);U(t)) - в этих точках касательный вектор к траектории меняет свое направление.

Григорий.