Здравствуйте, Валерий.
Продолжаем нашу плодотворную дискуссию.На повестке дня новая Модель Валерия, в которой он пытается ещё раз доказать, что добавленная стоимость, выраженная в денежных единицах фиксированной стоимости, сохраняется при росте уровня оплаты труда.
Сразу хочу подчеркнуть один пункт.Совершенно очевидно, что в модели с простым воспроизводством, где выпуски продукции фиксированы, выпуск второго подразделения ("жизненные средства") полностью потребляется рабочими и капиталистами. Поэтому потребление рабочих В НАТУРАЛЬНОМ ВЫРАЖЕНИИ плюс потребление капиталистов В НАТУРАЛЬНОМ ВЫРАЖЕНИИ всегда будет равно выпуску продукции второго подразделения. Более того, поскольку по условию задачи технологии фиксированы, то фиксирована и стоимость выпуска второго подразделения, а также стоимость каждой единицы продукции второго подразделения. Поэтому сумма СТОИМОСТИ продукции, потребляемой рабочими и капиталистами будет постоянна и не будет зависеть от уровня зарплаты. В этом смысле верно, что V + M = Const.
Приведённая выше интерпретация закона сохранения добавленной стоимости - совершенно тривиальный факт. Рикардо на этот счёт писал:
Цитата:
Если хлеб подлежит разделу между фермером и рабочим, то чем больше доля последнего, тем меньше остается первому» (Д. Рикардо, «Начала политической экономии», гл.1, отд.4).
Если фиксированное количество ПРОДУКТА (выраженное, например, в килограммах) делится на две части между рабочими и капиталистами, то чем больше достанется одним, тем меньше достанется другим. Количество продукта можно выразить не в килограммах, а в стоимости - в рабочих часах, например. Если стоимость единицы продукта фиксирована, то это тривиальное утверждение можно сформулировать ещё и так:
Чем большая стоимость достаётся рабочим, тем меньшая стоимость достаётся капиталистам.
В этом и состоит
истинный смысл "закона сохранения добавленной стоимости". Этот закон
должен быть сформулирован в терминах "количества продукта" или в терминах "стоимость продукта", выраженная в рабочих часах.Но стандартная версия ТТС неправомерно расширяет этот тривиальный закон, вводя в формулировку понятие прибыль и выражая "стоимость" в деньгах. Вот тут-то и начинаются нестыковки, потому что продукт второго подразделения, измеренный в денежных единицах фиксированной стоимости, будет меняться с изменением уровня оплаты труда, как это следует из рассмотрения модели, описание которой было приведено в предыдущих сообщениях.
Причина нестыковки в том, что цена единицы продукции второго подразделения меняется с изменением уровня оплаты труда, а стоимость единицы продукции НЕ МЕНЯЕТСЯ с изменением уровня оплаты труда. Но если продукт второго подразделения, выраженный как "стоимость", остаётся постоянным, то этот же продукт, выраженный в денежной форме будет меняться, так как меняется цена единицы продукта, хотя стоимость денег остаётся той же. В этом и состоит парадокс стандартной версии ТТС - она применяет для описания тривиального факта (деление фиксированной величины на две части) несоответствующие термины. Продукт второго подразделения в натуральном выражении фиксирован, но денежное выражение этого продукта зависит от уровня оплаты труда.
Поэтому
надо чётко различать продукт второго подразделения как фиксированную СТОИМОСТЬ и продукт второго подразделения как определённую СУММУ ДЕНЕГ. Первая величина остаётся неизменной с ростом зарплаты, вторая величина меняется. "Добавленная стоимость" понимаемая буквально, как СТОИМОСТЬ продукции второго подразделения, - СОХРАНЯЕТСЯ.
"Добавленная стоимость" как денежное выражение продукции второго подразделения, - НЕ СОХРАНЯЕТСЯ.Самый правильный путь для сторонника стандартной версии ТТС - отстоять закон V + M = Const состоит в том, чтобы применять термин "добавленная стоимость" только в первом значении, то есть интерпретировать символы V и M как стоимость двух частей продукции второго подразделения: V - стоимость продукта, достающегося рабочим и M - стоимость продукта, достающегося капиталистам. Именно брать эти величины как СТОИМОСТИ, выражая их через количество труда, но ни в коем случае В ДЕНЕЖНОЙ ФОРМЕ.
Как только сторонники стандартной версии ТТС пытаются придать термину V смысл заработной платы, а символу M смысл совокупной прибыли, они вступают в противоречие с математическими закономерностями модели капиталистической экономики с простым воспроизводством. Зарплата выражается В ДЕНЬГАХ, прибыль выражается В ДЕНЬГАХ, но мы знаем, что продукция второго подразделения, выраженая В ДЕНЬГАХ, зависит от уровня оплаты труда - от этого никуда не деться - это видно из системы уравнений для цен, в которых зависимость от уровня оплаты w сидит в явном виде:
(1) (a0*p1 + w * l0 * p2) * (1 + r) = 1
(2) (a1*p1 + w * l1 * p2) * (1 + r) = p1
(3) (a2*p1 + w * l2 * p2) * (1 + r) = p2
Я надеялся, что Валерий сам укажет на эту двойственность смысла термина "добавленная стоимость" и скорректирует закон сохранения добавленной стоимости соответствующим образом. Но, увы. Вместо этого простого и ясного разрешения проблемы, Валерий продолжает доказывать то, что доказать невозможно.
Валерий хочет доказать, что "добавленная стоимость" сохраняется и при втором значении этого термина, то есть, что сумма ЗАРПЛАТЫ и ПРИБЫЛИ остаётся постоянной при росте уровня оплаты труда. А это неверно.
Закон сохранения "добавленной стоимости" выполняется в следующей форме:УТВЕРЖДЕНИЕ 1: СТОИМОСТЬ ПРЕДМЕТОВ ПОТРЕБЛЕНИЯ РАБОЧИХ + СТОИМОСТЬ ПРЕДМЕТОВ ПОТРЕБЛЕНИЯ КАПИТАЛИСТОВ = Const = СТОИМОСТИ ВЫПУСКА ВТОРОГО ПОДРАЗДЕЛЕНИЯ.
Закон сохранения "добавленной стоимости", выраженный в денежной форме, НЕ выполняется:УТВЕРЖДЕНИЕ 2: ЗАРПЛАТА РАБОЧИХ + ПРИБЫЛЬ КАПИТАЛИСТОВ ≠ ConstУтверждение 1 - это совершенно тривиальный факт сохранения фиксированной величины, которую делят на две части.
Утверждение 2 - математическое следствие из анализа модели, воспроизводящей капиталистическую экономику с простым воспроизводством.
Валерий пытается доказать Утверждение 2 и предлагает математическую модель.
Рассмотрим его доказательство.
МОДЕЛЬ ВАЛЕРИЯ (копия сообщения от 25 февраля 2012 (10.54)).


КРИТИЧЕСКИЕ ПОЯСНЕНИЯ.ПУНКТ №1. С самого начала меня удивило и озадачило, почему Вы коэффициенты l1 и l2 называете: "технологические коэффициенты В.В. Калюжного"? Неужели Вы ни разу не встречали эти коэффициенты в публикациях? Есть множество книг и статей, авторы которых используют эти обозначения в том же самом смысле, что и Вы. Правда они при этом не пишут "коэффициенты Wolf" или "коэффициенты Abraham-Frois". Как-то нескромно получается.
ПУНКТ №2. Почему Вы решили, что коэффициенты c1 и с2 а также коэффициенты l1 и l2 должны удовлетворять соотношениям:
(2К) c1 + c2 = 1
(3К) l1 + l2 = 1
Ведь Ваши уравнения (1) описывают затраты труда
НА ЕДИНИЦУ продукции. Коэффициенты c1, с2, l1 и l2 характеризуют ТЕХНОЛОГИИ производства в первом и втором подразделениях. А технологии зависят от технических особенностей производства и вовсе не обязательно они должны удовлетворять условиям (2К) и (3К). В моей модели коэффициенты a1;a2;l1;l2 (аналог Вашей четвёрки c1, с2, l1 и l2) выбираются произвольно и при этом условия простого воспроизводства соблюдаются при любом их выборе. Условия баланса обеспечиваются соответствующим выбором объёмов выпуска продукции.
Ниже (см. ПУНКТ №6 в данном сообщении) будет показано, что Ваше условие (2К) эквивалентно предположению о равенстве объёмов выпуска продукции в обоих подразделениях.ПУНКТ №3. Наложив условия (2К)-(3К) Вы с самого начала сужаете постановку задачи, то есть рассматриваете лишь частный случай (одинаковый объём производства в первом и втором подразделениях).
ПУНКТ №4. Используя условие (2К), Вы выводите Вашу формулу (9), которая поэтому верна лишь для рассматриваемого Вами частного случая.
(9К) l1 + l2 = L2
Но Вы при этом интерпретируете эту формулу так, как если бы она относилась к продукции всего второго подразделения. Но Вы же пишите в самом начале, что у Вас значки l1; l2; L1: L2 относятся к ЕДИНИЦЕ ПРОДУКТА, а не к полному выпуску продукции.
В одном месте (сразу после Вашей формулы (1)) Вы пишите:
Цитата:
l1 и l2 - технологические коэффициенты..., характеризующие прямые затраты простого труда... на производство единицы товара подразделений I и II соответственно
В другом месте (сразу после Вашей формулы (9)) Вы пишите:
Цитата:
(9) l1 + l2 = L2
Таким образом, фундаментальным свойством простого воспроизводства является то, что сумма технологических коэффициентов l всегда равна стоимости продукта второго подразделения.
Правильно было бы, если бы Вы написали так: из предположения, что выполняется соотношение c1 + c2 = 1 следует, что стоимость ЕДИНИЦЫ продукции второго подразделения удовлетворяет соотношению: l1 + l2 = L2. Причём тут простое воспроизводство и причём тут стоимость продукции второго подразделения? При любом производстве, если выполняются Ваши уравнения (1) и условие (2), то выполняется и уравнение (9).
ПУНКТ №5. Дальше Вы переходите к анализу всей экономики.
Исправим сначала Ваши неточности.
Берём Ваши уравнения, которые описывают технологии производства ЕДИНИЦЫ продукта:
c1 * L1 + l1 = L1
c2 * L1 + l2 = L2
Умножим первое уравнение на выпуск продукции первого подразделения X1, а второе уравнение - на выпуск продукции второго подразделения X2. Получим:
(1Г) c1 * L1 * X1 + l1 * X1 = L1 * X1 - стоимость продукции первого подразделения
(2Г) c2 * L1 * X2 + l2 * X2 = L2 * X2 - стоимость продукции второго подразделения
Так как у нас простое воспроизводство, то получаем:
(3Г) c1 * X1 + c2 * X2 = X1 - условие простого воспроизводства.
Второе условие следует из первого:
(4Г) l1 * X1 + l2 * X2 = L2 * X2
Из (3Г) следует, что Ваше условие c1 + c2 = 1 выполняется лишь тогда, когда X1 = X2.Накладывая на коэффициенты условие c1 + c2 = 1, Вы неявно предполагаете, что выпуски продукции в первом и втором подразделениях одинаковы (например 100000 штук). Почему?
Можно, конечно, "выкрутиться" из этого затруднения, сказав, что мы с самого начала выбираем единицы продукции так, чтобы натуральные объёмы выпуска продукции первого и второго подразделения были бы равны: X1 = X2. Но Вы же этого не говорите - приходится доделывать за Вас вашу работу.
Итак имеем модель, в которой выпуски продукции одинаковы в натуральном выражении (это обеспечивается за счёт соответствующего выбора единиц измерения продукции). Теперь всё правильно (с моими замечаниями).
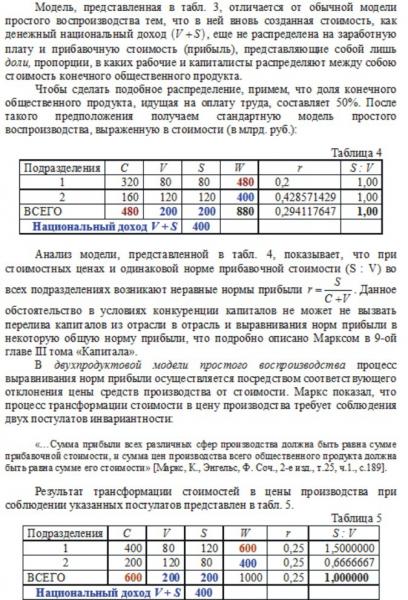
ПУНКТ №6. Строим числовой пример (Таблица 3) экономики. В этом примере X1 = X2 = 400. Дальше разбиваете добавленную стоимость на две части (Таблица 4). И потом начинаете "трансформировать" к ценам производства, так как "нормы прибыли" не равны. Всё. Вы опять свернули с верного пути на дорогу в никуда - снова пытаетесь интерпретировать постоянство "добавленной СТОИМОСТИ" как постоянство суммы "ЗАРПЛАТА + ПРИБЫЛЬ". Как только Вы от стоимости (в часах) переходите к стоимости (в деньгах) - всё, забудьте о законе сохранения добавленной стоимости.
Добавленная стоимость, выраженная в деньгах, НЕ СОХРАНЯЕТСЯ и я уже много раз приводил соответствующие графики и даже модель, которая это ясно демонстрирует.
ПУНКТ №7. Сравним, наконец, Ваши Таблицы 5 и 6. Я просто беру мой алгоритм нахождения технологических параметров (был приведён в предыдущих сообщениях) и вношу в него Ваши значения C1;C2;V1;V2; r из Таблицы 5 и Таблицы 6, считая, что выпуски продукции равны: X1 = X2 = 400. Задавая параметры l0 = 0.6; X2 = 400; a12 = a1 : a2 = 2; l1 = 0.5, находим:
Для Таблицы 5 получаем а0 = 0.3733. Для Таблицы 6 получаем а0 = 0.3785. То есть Ваше преобразование Таблицы 5 в Таблицу 6 эквивалентно изменению технологии производства денег, что недопустимо по условию задачи.С уважением,
Григорий.



