Уважаемый Инженер!Ваша модель расширенного воспроизводства примитивна и ни на что не годится. Это игрушка, которую ежегодно (от периода к периоду) можно умножать на 1,1 (вообще на любой коэффициент) и так до бесконечности. Новых знаний она не несет, а лишь вызывает недоумение.
В вашей модели норма прибыли определяется по элементам издержек, а не как отношение прибыли к
примененному капиталу. Норма прибыли, определяемая по элементам издержек производства, годится для иллюстрации первоначальных теоретических результатов Маркса, но не для практики. Об этом знают, по-видимому, даже студенты.
Предлагаю воспользоваться элементарной моделью расширенного воспроизводства, приводимой ниже, и показать, на что вы способны в макроэкономическом анализе
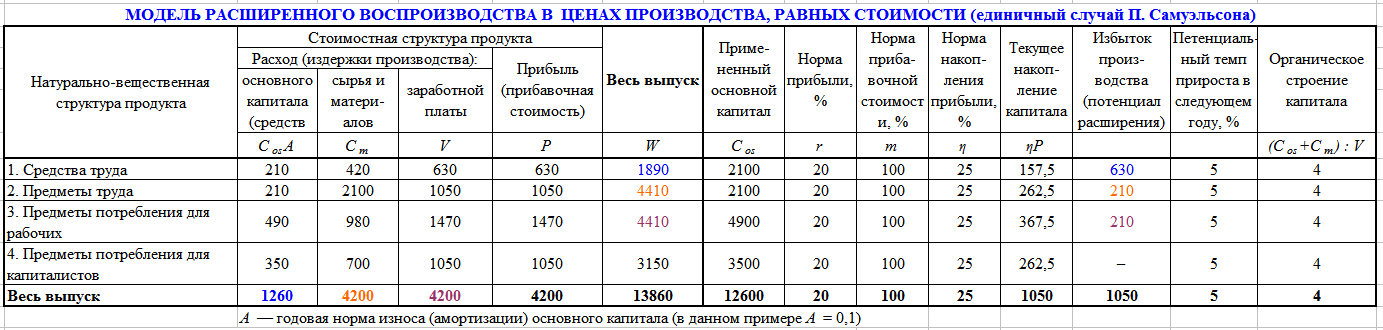
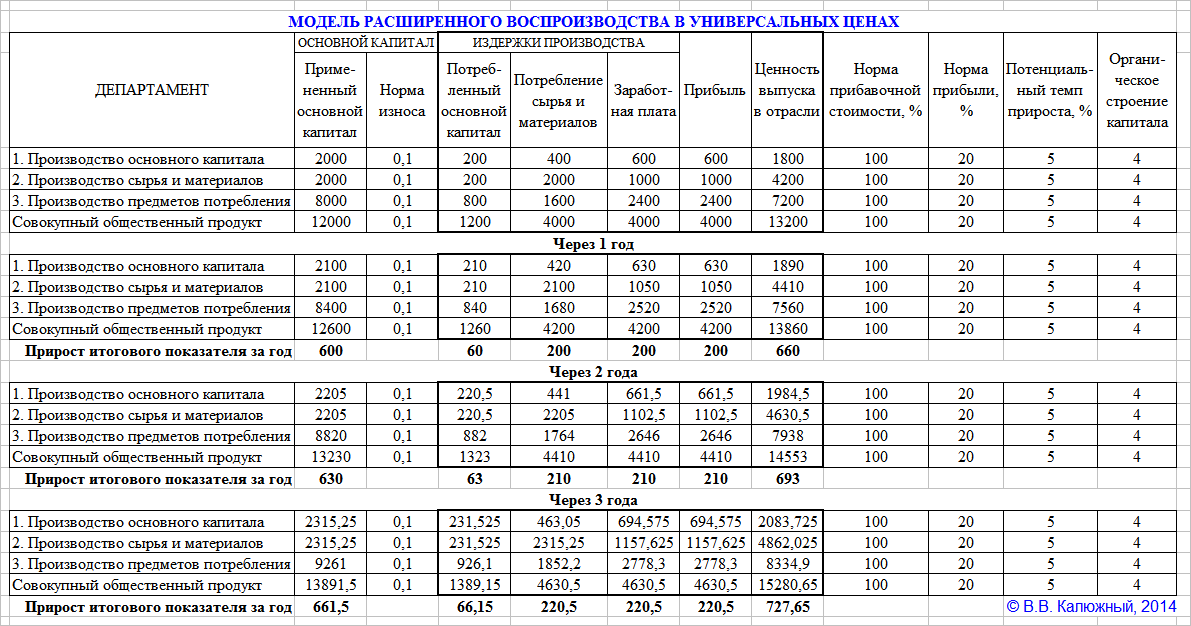
К сожалению, вам не хватает систематизированных знаний, чтений работ В.С. Немчинова, О. Ланге, В.С. Дадаяна и др. исследователей расширенного воспроизводства. Мне трудно с вами спорить ввиду отсутствия предмета спора. Вы не определяете новизну вашего исследования и думаете, что ваша модель — это последнее слово в науке. Возможно и последнее, но в вульгарной политэкономии.
Сконцентрирую внимание всего на одном нюансе. Во всех ваших числовых моделях органическое строение третьей отрасли совпадает со среднеотраслевым. Вам это, вообще говоря, абсолютно не надо. Но надо Григорию Сергеевичу, у которого собственно у первого и появились эти модели, которые я называю «заряженными».
Вопрос: вы заимствовали «заряженную» модель у Григория Сергеевича, или «случайно» так получилось именно у вас?
Все дело в том, что свойства «заряженной» модели, которой пользуется Григорий Сергеевич, ДАВНО ИЗВЕСТНЫ именно при решении трансформационной проблемы. Главное, при написании своей 100-страничной статьи «Решение проблемы трансформирования стоимостей в цены производства в модели простого воспроизводства с тремя подразделениями» он должен был четко заявить о том, что использует «заряженную матрицу».
Но этого нет. Вот текст заключения Г.С. Пушного по своей статье:
Цитата:
Особенности капиталистического производства на ранней стадии развития капитализма (торгово-купеческий капитализм) должны были приводить к выполнению нетривиальных условий баланса в ранней капиталистической экономике. При рассмотрении исторической проблемы трансформирования (превращения обмена по стоимости в обмен по ценам производства), мы должны поэтому накладывать нетривиальные условия баланса. Но в развитой капиталистической экономике проблема трансформирования в рамках моделей-1 и 2 не всегда имеет решение, так как в этом случае нетривиальные условия баланса могут нарушаться. В этом случае решение возможно лишь в рамках более реалистичной модели-4, в которой учитывается ТРУД КАПИТАЛИСТОВ.
Владислав Борткевич (Bortkiewicz (1907a)) в своей знаменитой статье, положившей начало столетним спорам о проблеме трансформирования, использовал модель-1, в которой проблема трансформирования имеет решение, если выполнены нетривиальные условия баланса Маркса. Если рассматривать ситуацию раннего капитализма, необходимо учитывать эти нетривиальные условия баланса, и тогда проблема трансформирования в рамках моделей1 и 2 имеет решение. Если не требовать выполнения нетривиальных условий баланса, то задачу надо рассматривать в рамках более реалистичной модели-4. При выполнении в модели-4 нетривиальных условий баланса, она может быть сведена к модели-2 и далее к модели-1.
Владислав Борткевич не учёл нетривиальных условий баланса, которые должны были выполняться в ранней капиталистической экономике. Отсюда и возникает (не оправданное при анализе ранней капиталистической экономики) расширение множества решений, для части из которых выполняется только одно правило трансформирования Маркса. Если же учесть нетривиальные условия баланса, то при обмене по ценам производства выполняются все правила трансформирования.
Решение проблемы трансформирования в рамках моделей -1 и 2 всегда существует, если выполняются нетривиальные условия баланса Маркса, но вследствие наложения этих условий, структура стоимостной матрицы должна быть специфицирована ограничениями (23) для модели-1 и (137) для модели-2. Следовательно, при выборе произвольной стоимостной структуры, удовлетворяющей лишь условиям тривиального баланса, в рамках моделей-1 и 2 решения нет.
Постановка задачи в рамках моделей-1 и 2 не учитывает труд капиталистов и влияние налоговой системы. Эти факторы учтены в модели-4 и в рамках этой модели решение всегда существует и без наложения нетривиальных условий баланса.
Проблему исторической трансформации можно ставить в рамках модели-1 с наложением нетривиальных условий баланса, поскольку в ранней капиталистической экономике эти условия должны были выполняться. Математически, проблема сводится к нахождению исторической траектории временно равновесных состояний, которая связывает равновесное состояние при обмене по стоимости и равновесное состояние при обмене по ценам производства. Каждой точке траектории временно равновесных состояний (temporary equilibrium states) соответствует определённая технология производства, которую можно описать заданием технологических параметров и нормы прибавочной стоимости19.
Проблема исторического трансформирования обмена по стоимости в обмен по ценам производства – это проблема трансформирования структуры стоимостной матрицы экономики. Как в действительности мог бы происходить процесс изменения технологий производства, который трансформировал бы стоимостную структуру (SV), соответствующую обмену по стоимости, в стоимостную структуру (SP), соответствующую обмену по ценам производства? Траектория эта (в пространстве технологических коэффициентов) должна быть выбрана так, чтобы норма прибыли на ней не убывала бы в процессе трансформирования одной структуры в другую. При этом должны выполняться «условия реалистичности» переходного процесса, отражающие исторический прогресс технологий (параметры должны иметь тенденцию роста) и ригидность (малую подвижность) нормы прибавочной стоимости, связанную с жёстким сопротивлением её изменению со стороны капиталистов и рабочих.
Мы показали, что в рамках модели-1 простого воспроизводства такое трансформирование могло иметь место за счёт технологических улучшений третьего подразделения (роста параметра 3) и незначительного увеличения нормы прибавочной стоимости. Трудно сказать, какой в действительности (в реальном историческом процессе, если он происходил) была траектория (в пространстве), которая трансформировала нужным образом структуру стоимостной матрицы. Но наш анализ показывает, что такие траектории были возможны, и процесс исторического трансформирования мог произойти без нарушения условий текущего равновесия и в соответствии с основными законами регулирования ранней капиталистической экономики.
Хотя решение в модели-4 существует всегда, реалистичное решение существует не при всех допустимых, согласно (184), стоимостных структурах (пример модели-4, не имеющей реалистичных решений приведён в Дополнении VIII). В моделях-1 и 2 приходится накладывать дополнительные ограничения на стоимостную структуру (нетривиальные условия баланса Маркса), чтобы получить решение. Модель-4 не требует явного наложения дополнительных условий. Решение здесь всегда существует и без наложения нетривиальных условий баланса, но не все решения при этом будут реалистичными. Существует целое множество стоимостных структур, для которых существует лишь не реалистичное решение (какие-то вычисляемые величины будут выходить за пределы области допустимых значений).
Можно предложить три объяснения этому свойству решений в модели-4: 1) исторически, трансформирование происходит, когда стоимостная структура такова, что существует реалистичное решение, 2) модель-4 всё ещё недостаточно реалистична и не учитывает какие-то важные моменты, 3) ПРОБЛЕМА ТРАНСФОРМИРОВАНИЯ ДЛЯ РЯДА СТОИМОСТНЫХ СТРУКТУР НЕ ИМЕЕТ РЕАЛИСТИЧНЫХ РЕШЕНИЙ.
Мы склонны придерживаться третьего объяснения. САМА ВОЗМОЖНОСТЬ ОТСУТСТВИЯ В МОДЕЛИ-4 РЕАЛИСТИЧНЫХ РЕШЕНИЙ ДЛЯ НЕКОТОРЫХ ДОПУСТИМЫХ (УСЛОВИЯМИ ТРИВИАЛЬНОГО БАЛАНСА) СТОИМОСТНЫХ СТРУКТУР УКАЗЫВАЕТ, ПО НАШЕМУ МНЕНИЮ, НА НЕОБХОДИМОСТЬ ГЛУБОКОГО ПЕРЕСМОТРА ФУНДАМЕНТАЛЬНЫХ ОСНОВ ДАННОГО ЭКОНОМИЧЕСКОГО НАПРАВЛЕНИЯ: ЕГО ОПРЕДЕЛЕНИЙ, ПОСТУЛАТОВ И ИНТЕРПРЕТАЦИЙ. СУЩЕСТВУЮЩАЯ СЕЙЧАС ИНТЕРПРЕТАЦИЯ ТРУДОВОЙ ТЕОРИИ СТОИМОСТИ НЕ ПОЗВОЛЯЕТ РАЗРЕШИТЬ ПРОБЛЕМУ ТРАНСФОРМИРОВАНИЯ ДАЖЕ В РАМКАХ САМОЙ РЕАЛИСТИЧНОЙ МОДЕЛИ-4. Есть стоимостные структуры, для которых нет реалистичных решений. Мы полагаем, что причина этого кроется не в недостатках модели-4, а в принятом сейчас способе истолкования основных терминов данного направления. Интерпретация современной трудовой теории стоимости неизбежно ведёт к проблеме трансформирования, которая даже в рамках модели-4 (наиболее приближенной к реальности) не всегда имеет реалистичное решение. По-видимому, решение проблемы трансформирования не может быть получено в рамках традиционной интерпретации теории стоимости, но, вероятно, оно может быть найдено, если выйти за пределы традиционных рамок, расширив их, посредством переосмысления основ этой теории.
И коту ясно, что С.Г. Пушной проблему трансформации не решил, а вместо этого пришел к утешающему самого себя выводу, что НЕОБХОДИМ ГЛУБОКИЙ ПЕРЕСМОТР ФУНДАМЕНТАЛЬНЫХ ОСНОВ ДАННОГО ЭКОНОМИЧЕСКОГО НАПРАВЛЕНИЯ: ЕГО ОПРЕДЕЛЕНИЙ, ПОСТУЛАТОВ И ИНТЕРПРЕТАЦИЙ. СУЩЕСТВУЮЩАЯ СЕЙЧАС ИНТЕРПРЕТАЦИЯ ТРУДОВОЙ ТЕОРИИ СТОИМОСТИ НЕ ПОЗВОЛЯЕТ РАЗРЕШИТЬ ПРОБЛЕМУ ТРАНСФОРМИРОВАНИЯ ДАЖЕ В РАМКАХ САМОЙ РЕАЛИСТИЧНОЙ МОДЕЛИ.
Бедный Маркс трижды перевернулся в гробу, так как понял, что его задвинули в "данное экономическое направление".
Правда, не так давно забрезжил свет в конце тоннеля. Написано ПРИЛОЖЕНИЕ К СТАТЬЕ: «Решение проблемы трансформирования стоимостей в цены производства в модели простого воспроизводства с тремя подразделениями».
http://www.socintegrum.ru/P_2011_1_ru.htmlВот аннотация:
Цитата:
Приведено доказательство единственности решения проблемы трансформирования для экономики простого воспроизводства с тремя департаментами (Модель-1) в виде симметричных матриц общественного воспроизводства, удовлетворяющих «нетривиальным условиям баланса». Рассмотрены возможные экономические причины условий симметрии. Приведено решение задачи «обратного трансформирования» (из цен производства в стоимости). ДОКАЗАНО, ЧТО ЗАДАЧА «ОБРАТНОГО ТРАНСФОРМИРОВАНИЯ» ИМЕЕТ РЕШЕНИЕ ЛИШЬ ПРИ УСЛОВИИ СИММЕТРИИ МАТРИЦЫ ОБЩЕСТВЕННОГО ВОСПРОИЗВОДСТВА (В ЦЕНАХ ПРОИЗВОДСТВА). ТЕМ САМЫМ ДОКАЗАНО, ЧТО НЕОБХОДИМЫМ И ДОСТАТОЧНЫМ УСЛОВИЕМ СУЩЕСТВОВАНИЯ РЕШЕНИЯ ПРОБЛЕМЫ ТРАНСФОРМИРОВАНИЯ В МОДЕЛИ-1 ЯВЛЯЕТСЯ СИММЕТРИЯ МАТРИЦЫ ОБЩЕСТВЕННОГО ВОСПРОИЗВОДСТВА (В ЦЕНАХ ПРОИЗВОДСТВА). Рассмотрены критические возражения, представленные в статье Калюжный В.В. (2014a). Приведён алгоритм восстановления технологической матрицы Леонтьева по матрице общественного воспроизводства Модели-1.
Более того, даже сделано следующее заключение по моим постам на форуме:
Цитата:
Подытоживая, перечислим основные ошибки, которые были допущены автором критической статьи Валерием Васильевичем Калюжным (2014a).
ОШИБКА №1. При решении математической задачи, какой является в данном случае проблема трансформирования внутри Модли-1, математические соотношения, полученные с помощью эквивалентных математических преобразований из других математических соотношений, НЕЛЬЗЯ интерпретировать в категориях «причина» - «следствие». Если 2 умножить на два равно четыре, то это не причина того, что четыре умножить на четыре равно шестнадцать и наоборот. Если a умножить на b есть c, то это не причина того, что верно соотношение a умножить на b минус c равно нулю. Это просто разные эквивалентные записи одной и той же математической зависимости. Если матрица в ценах производства симметрична, то из этого следует, что , что легко доказать. Но это не значит, что симметрия матрицы – «причина» равенства. ЕСЛИ , ТО МАТРИЦА В ЦЕНАХ ПРОИЗВОДСТВА СИММЕТРИЧНА (ТЕОРЕМА КАЛЮЖНОГО), НО ЭТО НЕ ЗНАЧИТ, ЧТО УСЛОВИЕ - «ПРИЧИНА» СИММЕТРИИ МАТРИЦЫ. Это значит лишь, что существует некоторая связь между элементами матрицы, полученной в результате трансформирования – связь, которую можно выразить либо как условия симметрии этой матрицы, либо как условие.
ОШИБКА №2. Главным при решении математической задачи является выяснение условий существования решения – при каких условиях решение задачи существует? В задаче трансформирования внутри Модели-1 таким условием является симметрия матрицы общественного воспроизводства в ценах производства. Это условие является необходимым (доказано в главе II данного Приложения) и достаточным (доказано в статье). ИЗ УСЛОВИЯ СИММЕТРИИ СЛЕДУЕТ РАВЕНСТВО СТОИМОСТНЫХ ОРГАНИЧЕСКИХ СТРОЕНИЙ (ФОРМУЛА (23) МОЕЙ СТАТЬИ), А ПРЯМОЕ РЕШЕНИЕ ЗАДАЧИ ПРИВОДИТ К РАВЕНСТВУ ОРГАНИЧЕСКИХ СТРОЕНИЙ ТРЕТЬЕГО ПОДРАЗДЕЛЕНИЯ СО СРЕДНИМ ОРГАНИЧЕСКИМ СТРОЕНИЕМ И ДЛЯ ТРАНСФОРМИРОВАННОЙ МАТРИЦЫ В ЦЕНАХ ПРОИЗВОДСТВА (ТАБЛИЦА 6(1) МОЕЙ СТАТЬИ). Оба эти результата являются математически доказанными утверждениями, а не произвольно придуманными допущениями или умышленно скрытыми предпосылками («троянскими конями»). Оба эти результата в разной форме выражают свойства реалистичных решений проблемы трансформирования. Возражения против выполнения равенства не имеют смысла, поскольку это равенство выражает свойства единственно возможных внутри данной модели реалистичных решений. Других реалистичных решений, не обладающих этим свойством, в данной Модели не существует. ВОЗРАЖАТЬ ПРОТИВ ЭТОГО – ЭТО ЗНАЧИТ ВОЗРАЖАТЬ ПРОТИВ МАТЕМАТИЧЕСКИ ДОКАЗАННОЙ ТЕОРЕМЫ НА ТОМ ОСНОВАНИИ, ЧТО ПОЛУЧЕННЫЙ В РЕЗУЛЬТАТЕ ДОКАЗАТЕЛЬСТВА РЕЗУЛЬТАТ «НЕ НРАВИТСЯ» АВТОРУ КРИТИЧЕСКОЙ СТАТЬИ. Но с этим уж ничего не поделаешь. Нравится, не нравится, а результат именно такой. Любое решение задачи будет удовлетворять этому свойству , а возражать против математики - довольно странное занятие.
Понимаете, если трансформация (в традиционной постановке) получается только для симметричной матрицы (причем только при ценах производства, а при стоимостях симметричность улетучивается как 2х2=4), то да здравствуют симметричные матрицы! Но вот незадача. Если трансформировать стоимости в цены производства, то неоткуда почерпнуть сведения о симметричности матрицы. Сначала надо трансформировать, глянуть, а потом уже трансформировать. Это все равно, что родить ребенка, посмотреть, что он негр, а потом задвинуть обратно за ненадобностью.
Ну а у Инженера и смотреть никуда не надо. У него ЦЕНА =СТОИМОСТИ, помноженной на постоянный коэффициент, и усё.
Вот такие они чудные теории рождаются на данном форуме.
С уважением,
В.К.
P.S. СПРАВКА
Дадаян Владислав Суренович (1933 - 1994) - окончил Московский государственный экономический институт в 1958 г. по специальности "Экономика промышленности", доктор экономических наук (1966 г.), профессор (1993 г.). Работал в системе Академии наук с 1958 года (СОПС, ПЭММ, ЦЭМИ). С 1963 г. по 1967 г. работал доцентом, профессором, заместителем заведующего кафедрой математических методов анализа экономики экономического факультета МГУ им. М.В.Ломоносова.
В ЦЭМИ РАН работал заведующим лабораторией. Область научных интересов - анализ и моделирование макроэкономических процессов, в т.ч. процессов расширенного воспроизводства, автор (совместно с В.С.Немчиновым)
алгоритма трансформации межотраслевого баланса в схемы расширенного воспроизводства, а также анализ и моделирование страновых и мирохозяйственных систем.



